(파이썬) 빅데이터 분석기사 실기 준비 - 제3유형

2023-06-20

Python, 빅데이터 분석기사 실기, 제3유형

Page content

작업형 3유형 최종정리

작업형1 : 3문제 (30점), 데이터 전처리
작업형2 : 1문제 (40점), 분류/회귀 예측 모델링
작업형3 : 2문제 (30점), 가설 검정

라이브러리 확인

파이썬에서 가설검정을 위한 통계와 관련된 라이브러리는 크게 2가지이다.
- scipy : SciPy는 수치 계산, 최적화, 선형 대수, 신호 및 이미지 처리, 통계 분석 등과 같은 과학적 계산 작업을 수행하는 데 사용됨
- statsmodels : Statsmodels는 통계 분석과 추정을 위한 파이썬 라이브러리로, 선형 회귀, 로지스틱 회귀, 시계열 분석, 비모수적 추정 등 다양한 통계 모델을 지원함.
SciPy와 Statsmodels는 각각의 독립성과 기능을 가지고 있으며, 과학적 계산과 통계 분석을 위한 파이썬 생태계에서 함께 사용되는 보완적인 라이브러리임.

주의

여기에서는 각 검정의 구체적인 원리 설명은 하지 않는다.
코드 위주로만 확인을 하도록 한다.

One Sample T-Test

가설검정
- 귀무가설 : 붓꽃의 sepal_length의 평균은 5.5이다.
- 대립가설 : 붓꽃의 sepal_length의 평균은 5.5이 아니다.

import seaborn as sns
import pandas as pd

iris_df = sns.load_dataset("iris")
iris_df.head()

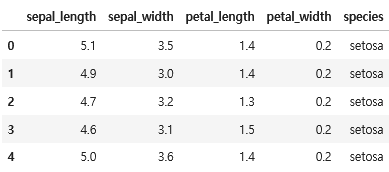
Untitled

문제 1.

sepal_length의 표본평균 X를 구하시오.

mu = iris_df['sepal_length'].mean()
round(mu, 2)

[결과]
5.84

문제 2.

위의 가설을 검정하기 위한 검정통계량을 구하시오.

from scipy import stats
from math import sqrt

t_statistic, p_value = stats.ttest_1samp(iris_df['sepal_length'], popmean=5.5)
print(round(t_statistic, 4))

[결과]
5.078

문제 3.

위의 통계량에 대한 p-값을 구하고(반올림하여 소숫점 넷째 자리까지 계산), 유의수준 0.05하에서 가설검정의 결과를 채택/기각 중 하나로 선택하시오.

if p_value >= 0.05:
    print("채택")
else:
    print("기각")

독립표본 T-검정

귀무가설 : male tip과 female tip의 평균은 같다.
대립가설 : male tip과 female tip의 평균은 다르다.

import seaborn as sns
import pandas as pd 

tips = sns.load_dataset("tips")
tips.head()

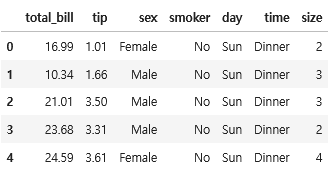
Untitled

문제 1.

male group의 표본평균, female group의 표본평균을 구하세요.

male = tips.loc[tips['sex'] == "Male", "tip"]
round(male.mean(), 2)

[결과]
3.09

female = tips.loc[tips['sex'] == "Female", "tip"]
round(female.mean(), 2)

[결과]
2.83

문제 2.

위의 가설을 검정하기 위한 검정통계량을 구하시오. (반올림하여 소숫점 둘째 자리까지 계산)

from scipy.stats import stats
t_statistic, p_value = stats.ttest_ind(male, female, equal_var=True)
print(round(t_statistic, 2))
print(round(p_value, 2))

[결과]
1.39
0.17

문제 3.

위의 통계량에 대한 p-값을 구하고 (반올림하여 소숫점 넷째 자리까지 계산), 유의수준 0.05하에서 가설검정의 결과를 채택/기각 중 하나로 선택하시오.

if p_value >= 0.05:
    print("채택")
else:
    print("기각")

[결과]
채택

대응표본 t검정

가상의 데이터를 만든다.

import pandas as pd
import numpy as np

# Set random seed for reproducibility
np.random.seed(0)

n = 50  # Sample size
before = np.random.normal(loc=10, scale=2, size=n)
mean_diff = 3 
after = before + mean_diff + np.random.normal(loc=0, scale=1, size=n)
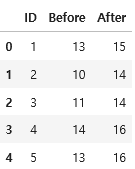
data = pd.DataFrame({'ID': range(1, n + 1), 'Before': before, 'After': after})
data['Before'] = data['Before'].astype("int")
data['After'] = data['After'].astype("int")
data.head()

Untitled

가설설정
- 귀무가설 : $\overline{\mu_{d}}$은 0이다.
- 대립가설 : $\overline{\mu_{d}}$은 0이 아니다.

문제 1.

표본평균 $\overline{\mu_{d}}$의 표본 평균을 구하시오. (반올림하여 소숫점 둘째 자리까지 계산)

diff = data['After'] - data['Before']
diff.mean()

[결과]
3.0

문제 2.

위의 가설을 검정하기 위한 검정통계량을 구하시오.

from scipy.stats import stats
from math import sqrt

t_statistic, p_value = stats.ttest_rel(data['Before'], data['After'])
print(round(t_statistic, 2))
print(round(p_value, 2))

[결과]
-23.48
0.0

문제 3.

위의 통계량에 대한 p-값을 구하고 (반올림하여 소숫점 넷째 자리까지 계산), 유의수준 0.05하에서 가설검정의 결과를 채택/기각 중 하나로 선택하시오.

if p_value >= 0.05:
    print("채택")
else:
    print("기각")

[결과]
기각

일원분산분석

각 종의 sepal_width 평균길이를 비교 분석 한다.
가설검정
- 귀무가설 : $\overline{X_{1}} = \overline{X_{2}} = \overline{X_{3}}$ 각 그룹의 평균은 모두 같다.
- 대립가설 : 적어도 한개의 그룹은 평균이 갖지 않다.
각 그룹의 데이터는 모두 정규성 그리고 등분산성은 만족하는 것으로 가정한다.

import seaborn as sns
import pandas as pd

iris_df = sns.load_dataset("iris")
iris_df.head()

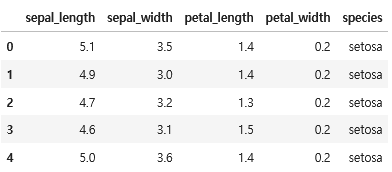
Untitled

데이터셋 분리

x1 = iris_df.loc[iris_df['species'] == "setosa", "sepal_width"]
x2 = iris_df.loc[iris_df['species'] == "versicolor", "sepal_width"]
x3 = iris_df.loc[iris_df['species'] == "virginica", "sepal_width"]

문제 1.

versicolor 종의 평균 꽃받침 너비를 구하시오. (반올림하여 소숫점 둘째 자리까지 계산)

x2.mean()

[결과]
2.7700000000000005

문제 2.

위의 가설을 검정하기 위한 검정통계량을 구하시오. (반올림하여 소숫점 둘째 자리까지 계산)

from scipy.stats import stats
f_statistic, p_value = stats.f_oneway(x1, x2, x3)
print(round(f_statistic, 2))
print(round(p_value, 2))

[결과]
49.16
0.0

문제 3.

위의 통계량에 대한 p-값을 구하고 (반올림하여 소숫점 넷째 자리까지 계산), 유의수준 0.05하에서 가설검정의 결과를 채택/기각 중 하나로 선택하시오.

if p_value >= 0.05:
    print("채택")
else:
    print("기각")

[결과]
기각

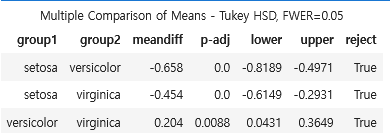
사후검정

대립가설 채택 시, 사후검정 진행

from statsmodels.stats.multicomp import pairwise_tukeyhsd
posthoc = pairwise_tukeyhsd(iris_df['sepal_width'], iris_df['species'])
posthoc.summary()

Untitled

카이제곱검정 독립성 검정

가설설정
- 귀무가설 : tips 데이터의 smoker와 day는 서로 관련성이 없다.
- 대립가설 : tips 데이터의 smoker와 day는 서로 관련성이 있다.

import seaborn as sns
import numpy as np

# 데이터 가져오기
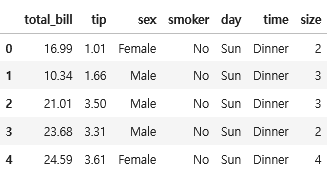
tips = sns.load_dataset("tips")
tips.head()

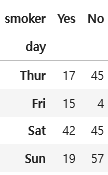
Untitled

분할표 만들기

observed = pd.crosstab(tips['day'], tips['smoker'])
observed

Untitled

문제 1.

주어진 데이터로 smoker와 day 분할표를 만들었을 때, yes가 가장 많은 day를 출력하세요.

result = observed.loc[observed['Yes'] == observed['Yes'].max()]
result.index[0]

[결과]
'Sat'

문제 2.

위의 가설을 검정하기 위한 검정통계량을 구하시오. (반올림하여 소숫점 둘째 자리까지 계산)

from scipy.stats import chi2_contingency

f_statistic, p_value, dof, expected = chi2_contingency(observed)
print(round(f_statistic, 4), round(p_value, 4))

[결과]
25.7872 0.0

X1 = observed.loc['Thur', :]
X2 = observed.loc['Fri', :]
X3 = observed.loc['Sat', :]
X4 = observed.loc['Sun', :]

result = chi2_contingency([X1, X2, X3, X4])
f_statistic, p_value = result[0], result[1]
print(round(f_statistic, 4), round(p_value, 4))

[결과]
25.7872 0.0

문제 3.

위의 통계량에 대한 p-값을 구하고 (반올림하여 소숫점 넷째 자리까지 계산), 유의수준 0.05하에서 가설검정의 결과를 채택/기각 중 하나로 선택하시오.

if p_value >= 0.05:
    print("채택")
else:
    print("기각")

[결과]
기각

카이제곱검정 적합성 검정

가설설정
- 귀무가설 : tips 데이터의 day 분포는 목요일 30%, 금요일 5%, 토요일 35%, 일요일 30%를 따른다.
- 대립가설 : tips 데이터의 day 분포는 목요일 30%, 금요일 5%, 토요일 35%, 일요일 30%를 따르지 않는다.

import seaborn as sns
import pandas as pd

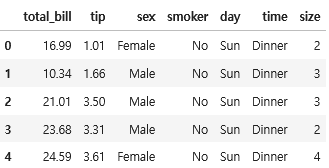
tips = sns.load_dataset("tips")
tips.head()

Untitled

문제 1.

day Sun의 분포에서 day Fri 분포 수를 뺀 값을 정수로 출력하시오.

count_df = tips.groupby("day").count()
count_df

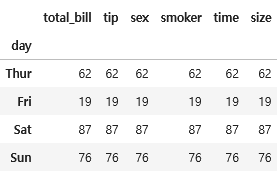
Untitled

result = count_df.loc['Sun', "total_bill"] - count_df.loc['Fri', "total_bill"]
result

[결과]
57

문제 2.

귀무가설에서 제시된 day 분포를 이용하여 기대 빈도를 계산하고, 위의 가설을 검정하기 위한 검정통계량을 구하시오. (반올림하여 소숫점 둘째 자리까지 계산)

total_sum = len(tips)
expected = [int(total_sum) * 0.3,  # 목요일
            int(total_sum) * 0.05, # 금요일
            int(total_sum) * 0.35, # 토요일
            int(total_sum) * 0.30  # 일요일
           ]
# 기대빈도 구하기
print(expected)

[결과]
[73.2, 12.200000000000001, 85.39999999999999, 73.2]

from scipy import stats

observed = count_df['total_bill'].values
f_score, p_value = stats.chisquare(observed, f_exp = expected)

print(round(f_score, 2), round(p_value, 2))

[결과]
5.64 0.13

문제 3.

위의 통계량에 대한 p-값을 구하고 (반올림하여 소숫점 넷째 자리까지 계산), 유의수준 0.05하에서 가설검정의 결과를 채택/기각 중 하나로 선택하시오.

if p_value >= 0.05:
    print("채택")
else:
    print("기각")

[결과]
채택

블로그 필자 신간 소개

Streamlit으로 프로젝트 한방에 끝내기 with 파이썬(2023, Sara & Evan)
많은 구매 부탁 드립니다.

책 판매 페이지

부크크 : https://www.bookk.co.kr/book/view/173250
교보문고 : https://product.kyobobook.co.kr/detail/S000202690179
예스 24 : https://www.yes24.com/Product/Goods/119627688
알라딘 : https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=318939281