ch04 - Modeling Visualisation

2020-05-15

Page content

개요

A picture is worth a thousand words — English Language Adage

The simple graph has brought more information to the data analyst’s mind than any other device. — John Tukey

한장의 그림이 수천단어보다 가치가 있다는 영어속담과, 명료한 시각화가 데이터분석가에게 다른 어떤 도구보다 더 많은 정보를 제공한다는 유명한 데이터 과학자의 조언. 핵심은 시각화이다.

본 장에서는 ggplot2 패키지를 활용한 시각화를 먼저 보여줄 것이다. 먼저 간단하게 ggplot2 패키지에 소개하자면 Grammar of Graphics¹의 철학을 담아서 R 생태계에서 유명한 학자 중, Hadley Wickham에 의해 주도적으로 개발되었다. 그래프에도 문법이 있다는 패키지의 철학 아래, R의 시각화는 괄목할만한 발전을 이루었고 이는 R의 대중화에도 큰 영향을 끼쳤다.

보통 시각화라고 하면 탐색적 자료 분석에 시각화를 많이 의미할 수도 있다. 그런데, 모델링 결과 또는 통계적인 결과를 시각화로 보여줄 수 있는 능력을 갖추는 것은 데이터분석가로써 한번 더 도약할 수 있다.

오늘 포스트는 이러한 주제에 맞춰서 다루도록 한다. 주요 이론적인 내용은 Hadley Wickham의 R for Data Science를 참고했다.

I. 사전준비

본 장에서는 시각화를 위해서 ggplot2를 주요 패키지로 사용한다. ggplot2 패키지를 설치했다고 가정한다. 만약 처음 패키지를 설치하는 사람이라면 R 패키지 설치에서 다시 한번 R 패키지 주요 생태계에 대해 이해하도록 한다.

II. 모델의 정의

통계에서 모델은 무엇일까? 또는 통계에서 모델의 역할은 무엇일까? 학자마다, 또는 주어진 환경에 따라 다르게 정의될 수도 있지만,

기본적으로 모델은 데이터의 특유의 알고리즘을 통해 일반적인 패턴을 가장 잘 요약해주는 일종의 summary와 같은 기능이다라고 정의할 수 있다.

보통 모델이 true or not true 이렇게 인식될 수도 있다. 그러나, 모델은 true or not true로 인식되기 보다는 useful or not useful로 판단하는 것이 좋다. 즉, 쓸만한 모형을 찾는 과정이 modeling이라고 할 수 있겠다.

III. 모델링 시각화

모형 학습을 위해서 필요한 필수 패키지를 설치한다.

library(tidyverse)
library(modelr)
library(moderndive)
options(na.action = na.warn)

(1) Sample 데이터 추출

evals 데이터에서 20개 정도의 데이터만 추출한다.

set.seed(1234) # 재현성
sample_20 <- evals %>% 
  sample_n(20) %>% 
  select(bty_avg, score)

(2) 250개의 모형

evals 데이터에 있는 2개의 변수를 활용해서 산점도를 그려본다.

x축은 bty_avg
y축은 score

ggplot(sample_20, aes(x = bty_avg, y = score)) + 
  geom_point()

데이터를 보면, 가운데 기준으로 위쪽으로 데이터가 모여 있는 것을 볼 수 있다.
이 때, 양변수가 만나는 점을 설명할 수 있는 모형을 만들어보자.
보통 이러한 관계를 선형 관계라고 표현한다. $$ y = a_0 + a_x \times x $$

위 데이터에 접하는 모형 250개를 만들어 보자.

models <- tibble(
  a1 = runif(250, 0.5, 4),
  a2 = runif(250, -.5, 1)
)

ggplot(sample_20, aes(x = bty_avg, y = score)) + 
  geom_abline(aes(intercept = a1, slope = a2), data = models, alpha=1/4) + 
  geom_point(color = "blue", alpha = 2/4) + 
  theme_bw()

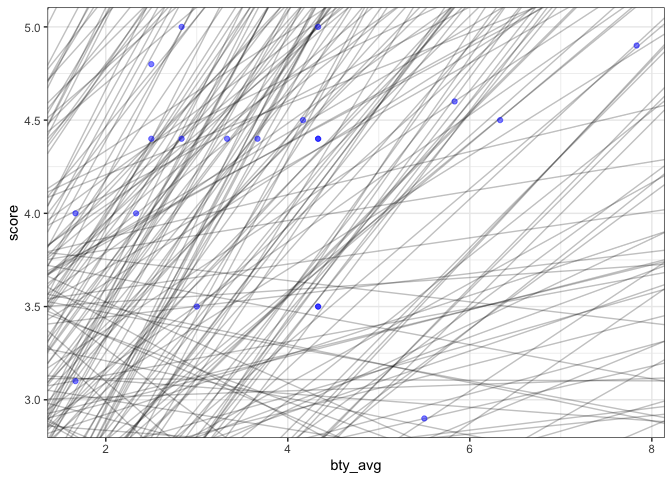
위 그림에서 보는 것처럼 굉장히 다양한 모형을 만들면서 최적의 모형을 찾는 과정이 데이터 분석의 프로세스라고 보면 좋다.

(3) 최적의 모형 찾기

최적의 모형은 어떻게 찾을 수 있을까?

최적의 모형을 찾으려면 ggplot2 패키지 내 geom_smooth()를 사용할 수 있다. 그러나, 문제는 geom_smooth를 사용하면 시각적으로는 결과적으로는 도움이 되지만, 실제 중간과정은 생략되었기 때문에 설명 부분에서는 조금 아쉬움이 있다.

이 부분이 오늘 과정의 핵심이며, 1차원 함수의 기울기와 상수를 찾는 것을 ggplot2 패키지를 활용해본다.

ggplot(sample_20, aes(x = bty_avg, y = score)) + 
  geom_point(color = "blue", alpha = 2/4) + 
  geom_smooth(method = "lm", se=FALSE)

## `geom_smooth()` using formula 'y ~ x'

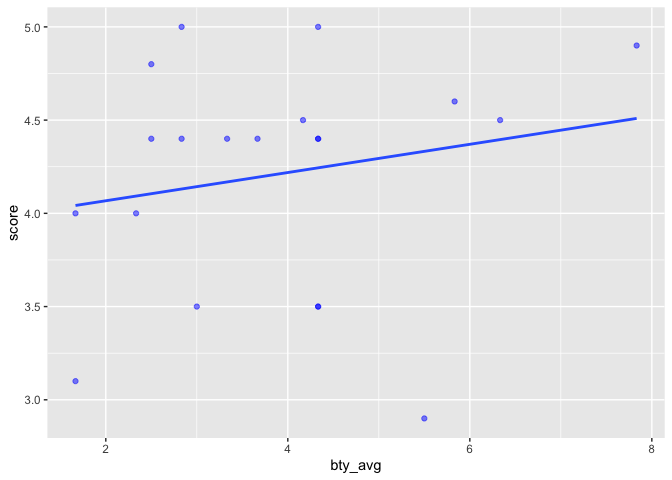
(4) Computing Distance

최적의 모형을 찾은 다음에 각각의 모형으로 각 점들이 얼마나 떨어졌는지 확인하는 함수를 작성한다.
3가지 함수가 필요하다.
model_1
measure_distance
eval_dist

model_1 <- function(a, data) {
  a[1] + data$bty_avg * a[2]
}

위 함수는 기울기와 상수를 정의하는 단순 회귀 모형 함수를 만든 것이다.
a[1]은 상수를 의미한다.
a[2]은 기울기를 의미한다.
data$bty_avg는 입력값을 의미한다.

measure_distance <- function(mod, data) {
  diff <- data$score - model_1(mod, data)
  sqrt(mean(diff^2))
}

measure_distance(c(3, 2), sample_20)

## [1] 7.23253

최적의 모형을 찾을 때 RMSE이라는 평균 제곱근 오차라는 통계적인 평가지표를 활용한다.
위 함수는 기울기(=3)와 상수(=2)를 적용해서 데이터 sample_20에 대한 RMSE 값을 측정한 결과는 7.23253 이 나왔다.

(5) All model dist

이제 전체 데이터와 모형간의 거리를 계산한다.

all_model_dist <- function(a1, a2) {
  measure_distance(c(a1, a2), sample_20)
}

models2 <- models %>% 
  mutate(dist = purrr::map2_dbl(a1, a2, all_model_dist))

models2 %>% head(5)

## # A tibble: 5 x 3
##      a1     a2  dist
##   <dbl>  <dbl> <dbl>
## 1 0.640  0.699 1.42 
## 2 1.27  -0.461 4.85 
## 3 3.34   0.260 0.666
## 4 2.34   0.732 1.53 
## 5 3.70   0.317 1.00

(6) Best 5 model

위 데이터를 근거로 가장 좋은 모델 5개를 찾는 그래프를 작성한다.

ggplot(sample_20, aes(x = bty_avg, y = score)) + 
  geom_point(size = 2, colour = "grey30") + 
  geom_abline(
    aes(intercept = a1, slope = a2, colour = -dist), 
    data = filter(models2, rank(dist) <= 5)
  )

위 그래프는 주어진 데이터에서 가장 좋은 모형 5개를 확인할 수 있다.

(7) 최적의 모형 찾기

이제 optim() 함수를 활용해서 최적의 기울기와 상수를 찾아보도록 한다.

best <- optim(c(0, 0), measure_distance, data = sample_20)

best$par

## [1] 3.91539624 0.07585949

기울기와 상수를 적용하여 다시 ggplot2 그래프를 작성한다.

ggplot(sample_20, aes(bty_avg, score)) + 
  geom_point(size = 2, colour = "grey30") + 
  geom_abline(intercept = best$par[1], slope = best$par[2])

실제로 lm 함수를 활용해여 기울기와 상수를 구해보자.

lm_mod <- lm(score ~ bty_avg, data = sample_20)

coef(lm_mod)

## (Intercept)     bty_avg 
##  3.91595907  0.07572129

실제로 best에서 추출한 것과, lm 함수를 사용한 값과 동일한 것을 확인할 수 있다.

IV. 결론

이번 포스트의 목적은 ggplot2 패키지를 활용하여 최적의 모형을 찾는 과정을 살펴 봤다.
시각화는 이렇게 모형을 찾는 과정도 넣을 수 있는데, 이러한 시각화를 활용하면 보다 효율적으로 선형회귀 모형에 대해 설명을 할 수 있다.

V. Reference

Grolemund, G., & Wickham, H. (n.d.). R for Data Science. Retrieved from https://r4ds.had.co.nz/

R 강의 소개

필자의 강의: 왕초보 데이터 분석 with R
- 쿠폰 유효일은 2021년 10월 30일까지입니다.
- 링크: https://www.udemy.com/course/beginner_with_r/?couponCode=5BF397C9A1E46079627D
- 현재 강의를 계속 찍고 있고, 가격은 한 Section이 끝날 때마다 조금씩 올릴 예정입니다.

Hadley Wickham이 작성한 ggplot2 패키지에 관한 논문을 읽어보는 것을 제안한다. “The Layered Grammar of Graphics”, http://vita.had.co.nz/papers/layered-grammar.pdf ↩︎