Tensorflow 2.0 Tutorial ch9.3 - 클러스터링
공지
-
본 Tutorial은 교재
시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다. -
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶으신 분은 반드시 교재를 구매하실 것을 권해드립니다.

- 본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.
Tutorial
이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.
- Google Colab Tensorflow 2.0 Installation
- Tensorflow 2.0 Tutorial ch3.3.1 - 난수 생성 및 시그모이드 함수
- Tensorflow 2.0 Tutorial ch3.3.2 - 난수 생성 및 시그모이드 함수 편향성
- Tensorflow 2.0 Tutorial ch3.3.3 - 첫번째 신경망 네트워크 - AND
- Tensorflow 2.0 Tutorial ch3.3.4 - 두번째 신경망 네트워크 - OR
- Tensorflow 2.0 Tutorial ch3.3.5 - 세번째 신경망 네트워크 - XOR
- Tensorflow 2.0 Tutorial ch4.1 - 선형회귀
- Tensorflow 2.0 Tutorial ch4.2 - 다항회귀
- Tensorflow 2.0 Tutorial ch4.3 - 딥러닝 네트워크를 이용한 회귀
- Tensorflow 2.0 Tutorial ch4.4 - 보스턴 주택 가격 데이터세트
- Tensorflow 2.0 Tutorial ch5.1 - 분류
- Tensorflow 2.0 Tutorial ch5.2 - 다항분류
- Tensorflow 2.0 Tutorial ch5.3 - Fashion MNIST
- Tensorflow 2.0 Tutorial ch6.1-2 - CNN 이론
- Tensorflow 2.0 Tutorial ch6.3 - Fashion MNIST with CNN 실습
- Tensorflow 2.0 Tutorial ch6.4 - 모형의 성능 높이기
- Tensorflow 2.0 Tutorial ch7.1 - RNN 이론 (1)
- Tensorflow 2.0 Tutorial ch7.1 - RNN 이론 (2)
- Tensorflow 2.0 Tutorial ch7.3 - 긍정, 부정 감성 분석
- Tensorflow 2.0 Tutorial ch7.4 - (1) 단어 단위 생성
- Tensorflow 2.0 Tutorial ch7.4 - (2) 단어 단위 생성
- Tensorflow 2.0 Tutorial ch8.1 - 텐서플로 허브
- Tensorflow 2.0 Tutorial ch8.2 - 전이 학습과 & Kaggle 대회
- Tensorflow 2.0 Tutorial ch8.3.1 - 컨볼루션 신경망을 사용한 텍스처 합성
- Tensorflow 2.0 Tutorial ch8.3.2 - 컨볼루션 신경망을 사용한 신경 스타일 전이
- Tensorflow 2.0 Tutorial ch9.1-2 - 오토인코더 & MNIST
I. 개요
- 오토인코더(
AutoEncoder)는 입력에 대한 출력을 학습해야 한다는 점은 기존 지도학습 네트워크와 동일합니다. - 그러나 그 출력이 입력과 동일하다는 점이 조금 다릅니다.
- 오토인코더는 자기 자신을 재생성하는 네트워크입니다.
-
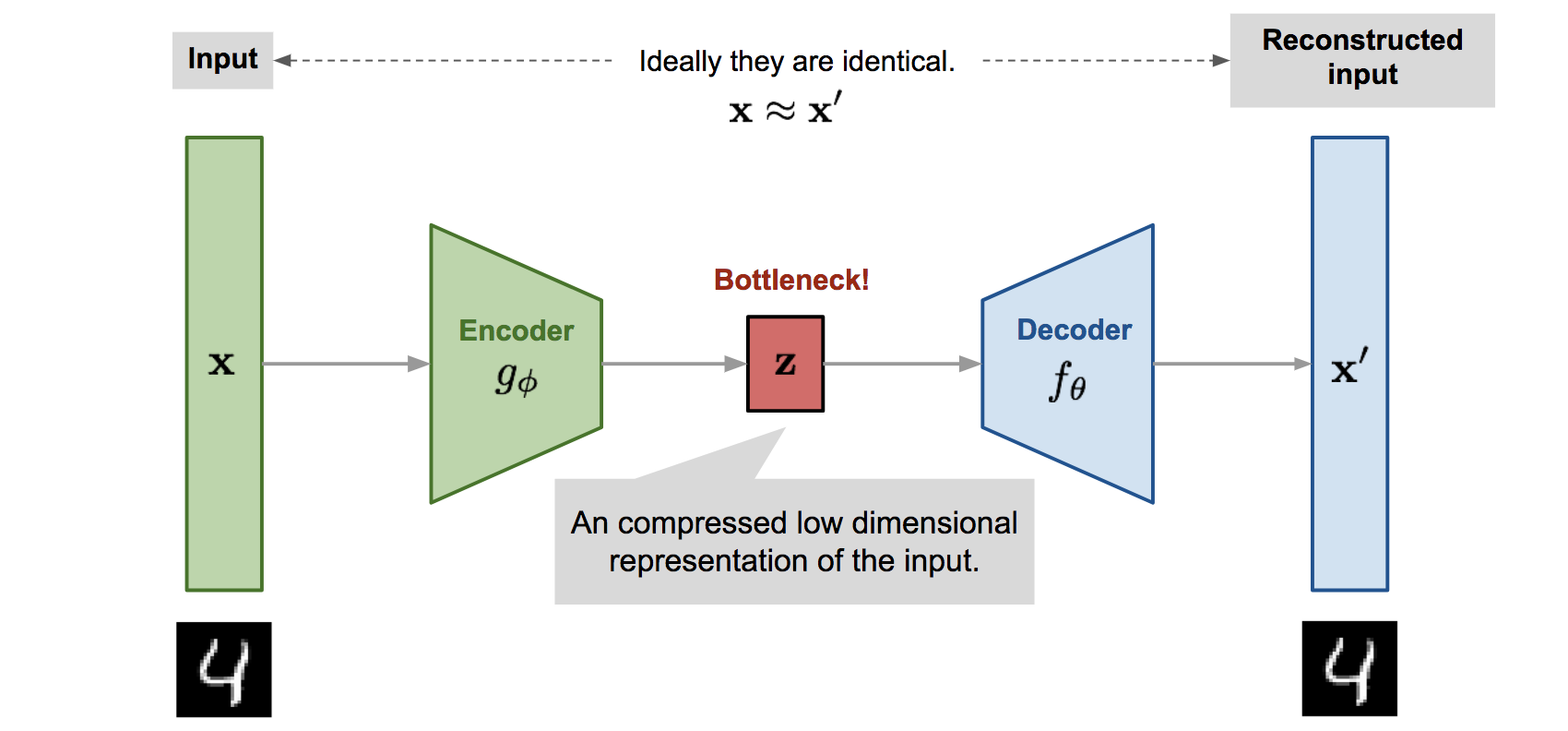
위 그림에서 보는 것처럼, 오토인코더는 크게 3가지 부분으로 구성됩니다.
z는 잠재 변수(Latent Vector)를 중심으로, 입력에 가까운 부분을 인코더(Encoder), 출력에 가까운 부분을 디코더(Decoder)라 분류합니다.
-
인코더의 역할은
입력에서잠재 변수를 만드는 것입니다. -
디코더의 역할은
잠재 변수를출력으로 만드는 것입니다. -
위 그림이 잠재변수를 기준으로 하나의 대칭구조를 이루는 것처럼, 레이어 역시 대칭되는 구조로 쌓아올려서 만듭니다.
-
음. 조금 쉽게 얘기하면, 오토인코더는 일종의 파일 압축과 유사합니다. 압축 파일은 압축하기 전과 압축을 해제한 뒤의 내용이 동일합니다. 컴퓨터공학 용어로 이러한 내용을 비손실 압축이라고 합니다. 내용적으로는 그러합니다.
-
그러나,
$x$와$x^i$의 차이점처럼 유사하지만 동일하지는 않습니다. 즉, 오토인코더는 손실 압축이라고 표현합니다. -
딥러닝 생성 모델 중 최근 가장 주목받고 있는 적대적 생성 모델(
Generative Adversarial Network이하GAN)의 생성자에서는 랜덤하게 생성된 변수를 잠재변수처럼 활용해서 새로운 이미지를 얻습니다.
II. 클러스터링
클러스터링은 대표적인 비지도학습 방법의 한 종류입니다. 비지도학습은 입력에 대한 출력이 존재하지 않습니다. 비지도학습과 관련된 문제는 다음과 같은 예로 표현할 수 있습니다.
- 사람의 얼굴 이미지를 몇 개의 집단으로 분류하는 것이 적절할까요?
- 단편 소설의 장르를 몇 개로 구분해야 할까요?
쉽게 답을 내기 어렵습니다. 그러나, 클러스터링 알고리즘을 이용해 군집을 나누는 시도를 해볼 수 있습니다.
K-평균 클러스터링은 주어진 입력 중 K개의 클러스터 중심을 임의로 정한 다음에 각 데이터와 K개의 중심과의 거리를 비교해서 가장 가까운 클러스터로 배당하고, K개의 중심의 위치를 해당 클러스터로 옮긴 후, 이를 반복하는 알고리즘입니다.
(1) 모듈 설치 및 데이터세트 확인
- 데이터는 (
train_X,train_Y), (test_X,test_Y)처럼 훈련 데이터와 테스트 데이터의 튜플 쌍으로 불러 올 수 있습니다. - 데이터를 로드한 후에
train_X와test_X를 255.0으로 나눠서 픽셀 정규화를 하게 됩니다. - 데이터가 잘 불러와졌는지 시각화를 통해 확인합니다.
# 텐서플로 2 버전 선택
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import numpy as np
import pandas as pd
import tensorflow_hub as hub
import matplotlib.pyplot as plt
import cv2
(train_X, train_Y), (test_X, test_Y) = tf.keras.datasets.mnist.load_data()
print(train_X.shape, train_Y.shape)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
(60000, 28, 28) (60000,)
train_X = train_X / 255.0
test_X = test_X / 255.0
plt.imshow(train_X[0].reshape(28, 28), cmap='gray')
plt.colorbar()
plt.show()
print(train_Y[0])
/img/tensorflow2.0/tutorial_09_03/
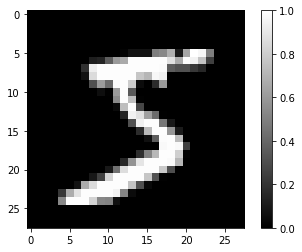
5
MNIST는Fashion MNIST처럼 가로와 세로가 각각 28픽셀인 흑백 이미지를 입력으로 하고, 0~9까지의 숫자를 출력으로 합니다. (5장과 6장 참조)
(2) 잠재변수 분리 모델
- 잠재변수를 분리할 수 있는 모델을 만듭니다.
- 지난시간에 학습했던
elu모델의 가중치를 그대로 사용하고, 8장에 등장했던 함수형API를 이용해서 만듭니다. 입력은model의 입력을 그대로 사용하고, 출력은 4번째 레이어의 (3번째 인덱스)의Dense레이어의 출력을 사용합니다.
train_X = train_X.reshape(-1, 28, 28, 1)
test_X = test_X.reshape(-1, 28, 28, 1)
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(filters=32, kernel_size=2, strides=(2,2), activation='elu', input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(filters=64, kernel_size=2, strides=(2,2), activation='elu'),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation='elu'),
tf.keras.layers.Dense(7*7*64, activation='elu'),
tf.keras.layers.Reshape(target_shape=(7,7,64)),
tf.keras.layers.Conv2DTranspose(filters=32, kernel_size=2, strides=(2,2), padding='same', activation='elu'),
tf.keras.layers.Conv2DTranspose(filters=1, kernel_size=2, strides=(2,2), padding='same', activation='sigmoid')
])
model.compile(optimizer=tf.optimizers.Adam(), loss='mse')
model.fit(train_X, train_X, epochs=20, batch_size=256)
Epoch 1/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0532
Epoch 2/20
235/235 [==============================] - 2s 6ms/step - loss: 0.0181
Epoch 3/20
235/235 [==============================] - 2s 6ms/step - loss: 0.0114
Epoch 4/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0094
Epoch 5/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0085
Epoch 6/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0080
Epoch 7/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0076
Epoch 8/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0073
Epoch 9/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0071
Epoch 10/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0070
Epoch 11/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0069
Epoch 12/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0067
Epoch 13/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0065
Epoch 14/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0064
Epoch 15/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0063
Epoch 16/20
235/235 [==============================] - 2s 6ms/step - loss: 0.0062
Epoch 17/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0061
Epoch 18/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0059
Epoch 19/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0058
Epoch 20/20
235/235 [==============================] - 2s 7ms/step - loss: 0.0056
<tensorflow.python.keras.callbacks.History at 0x7f724b0a5be0>
- 한줄로 모델을 만들고 훈련 데이터를 64차원의 잠재변수로 만듭니다.
latent_vector_model = tf.keras.Model(inputs=model.input, outputs=model.layers[3].output)
latent_vector=latent_vector_model.predict(train_X)
print(latent_vector.shape)
print(latent_vector[0])
(60000, 64)
[ 8.581287 13.880566 -0.9973878 -0.99999976 17.375837 -0.9999998
21.470583 7.486889 10.730955 17.930098 -0.9999982 -0.999995
18.012827 -0.99999994 10.878519 0.84252346 12.058126 -0.9999992
-0.9999996 -0.99999964 10.97095 8.179257 10.740526 2.934045
15.918473 6.9685793 -0.9999925 15.430024 5.45632 13.583059
11.942195 3.0618956 8.68406 7.022519 3.3600893 -0.22935408
-0.9999999 21.116535 5.195381 21.416206 11.435531 -0.9999959
12.934925 8.710132 16.295168 -0.9999958 9.566681 -0.9999999
-0.9999997 11.260084 3.3911107 15.630404 12.752275 21.86347
-0.9999942 7.3721986 11.828167 12.603353 6.7158327 9.415517
-0.9999996 -0.99998534 3.7850168 -0.9999999 ]
(3) 사이킷런의 K-평균 클러스터링 알고리즘 사용
- 이제 이 잠재변수에
K-평균 클러스터링알고리즘을 사용해 클러스터링을 시도합니다. 이 때에는scikit-learn라이브러리를 활용합니다.
%%time
from sklearn.cluster import KMeans
kmeans=KMeans(n_clusters=10, n_init=10, random_state=42)
kmeans.fit(latent_vector)
CPU times: user 12.7 s, sys: 3.06 s, total: 15.8 s
Wall time: 12 s
Wall Time은 실제로 걸린 시간을 의미하며, CPU Time은 멀티 코어 사용시 모든 코어의 계산 시간을 합쳐서 표시합니다.
(4) 계산 결과 및 클러스터링 결과 출력
다음과 같은 코드로 계산 결과를 확인합니다.
print(kmeans.labels_)
print(kmeans.cluster_centers_.shape)
print(kmeans.cluster_centers_[0])
[0 1 5 ... 3 8 3]
(10, 64)
[12.022522 12.878943 -0.9730305 -0.99999547 11.162719 -0.99999875
10.717042 4.197002 10.867007 10.656286 -0.9999948 -0.9999962
11.743372 -0.9999997 18.646065 2.8977199 12.208149 -0.9999985
-0.9999977 -0.9999986 9.804234 10.8237 11.522504 14.51758
12.841155 8.481935 -0.99997735 12.95512 9.044333 12.863187
15.309784 8.42041 4.893768 9.139908 4.298092 9.0015545
-0.9999992 16.420288 12.175448 17.10225 11.114536 -0.9999808
17.079649 14.277916 14.1573305 -0.9999922 11.437085 -0.9999989
-0.9999989 15.305092 7.9359035 11.408762 9.687219 14.03581
-0.99999744 10.3641405 12.274414 12.197285 8.345043 11.521661
-0.9999953 -0.99990386 12.515451 -0.9999994 ]
labels_에는 각 데이터가 0부터 9사이의 어떤 클러스터에 속하는지에 대한 정보가 저장됩니다.cluster_cetners_에는 각 클러스터의 중심 좌표가 저장되고, 잠재변수와 마찬가지로 64차원이기 때문에 이 좌표가 각각 무엇을 의미지하는지 직관적으로 알기 어렵습니다.- 각 클러스터에 속하는 이미지가 어떤 것인지 출력합니다.
import random
plt.figure(figsize=(12,12))
for i in range(10):
images=train_X[kmeans.labels_ == i]
for c in range(10):
plt.subplot(10, 10, i*10+c+1)
plt.imshow(images[c].reshape(28, 28), cmap='gray')
plt.axis('off')
plt.show()

- 출력 이미지의 각 행은 0번 클러스터, 1번 클러스터, …, 9번 클러스터를 나타냅니다.
- 그런데, 숫자가 다르면서 같은 클러스터로 분류된 이미지들이 문제입니다.
- 잠재변수의 차원수를 늘리거나
KMeans()의n_init을 늘려서 좀 더 분류가 잘 되도록 시도해볼 수 있습니다. - 그러나, 여전히 클러스터링 결과를 시각화를 해야 문제가 남고, 이를 시행하려면 2차원 또는 3차원의 잠재변수가 가진 자원을 축소해야 합니다.
(5) t-SNE의 개념
-
t-SNE는 강력한 시각화 도구로 고차원의 데이터를 저차원(주로 2차원 혹은 3차원)의 시각화를 위한 데이터로 변환합니다.
-
K-평균 클러스터링이 클러스터를 계산하기 위한 단위로 중심과 각 데이터의 거리를 계산하는 데 비해,
t-SNE는 각 데이터의 유사도를 정의하고, 원래 공간에서 유사도와 저차원 공간에서의 유사도가 비슷해지도록 학습시킵니다. -
SNE는Stochastic Neighbor Embedding의 약자로, 여기에서 유사도는 확률적(Stochastic)으로 표현됩니다.t는t-분포를 나타냅니다. -
t-분포와 정규분포의 모양 차이 그래프
import scipy as sp
t_dist = sp.stats.t(2.74)
normal_dist = sp.stats.norm()
x = np.linspace(-5, 5, 100)
t_pdf = t_dist.pdf(x)
normal_pdf = normal_dist.pdf(x)
plt.plot(x, t_pdf, c='red', label='t-dist')
plt.plot(x, normal_pdf, c='blue', label='normal-dist')
plt.legend()
plt.show()
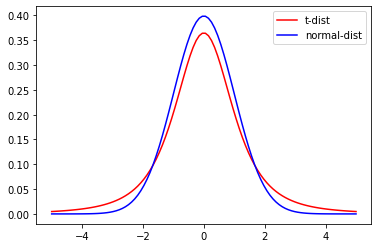
- t-분포는 정규분포와 비슷하게 생겼지만 중심이 좀 더 낮고 꼬리가 좀 더 두꺼운 분포이입니다.
- 거리를 확률로 표현한다는 것은 데이터 하나를 중심으로 다른 데이터를 거리에 대한
t-분포의 확률로 치환시키는 것입니다. - t-SNE 알고리즘의 주요 핵심 내용은 고차원과 저차원에서 확률값을 각각 구한 다음, 저차원의 확률값이 고차원에 가까워지도록 학습시키는 것입니다.
%%time
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, learning_rate=100, perplexity=15, random_state=0)
tsne_vector=tsne.fit_transform(latent_vector[:5000])
CPU times: user 1min, sys: 499 µs, total: 1min
Wall time: 32.7 s
tsne = TSNE(n_components=2, learning_rate=100, perplexity=15, random_state=0)
- n_components는 저차원의 수를 의미합니다. 2차원 공간이기 때문에 2를 넣습니다.
- learning_rate는 학습률로 10에서 1000사이의 큰 숫자를 넣습니다.
- perplexity는 알고리즘 계산에서 고려할 최근접 이웃의 숫자이며, 보통 5-50사이의 숫자를 넣습니다.
random_state는 KMeans와 마찬가지로 랜덤 초기화 숫자입니다.
tsne_vector=tsne.fit_transform(latent_vector[:5000])
- TSNE는 학습과 변환 과정을 동시에 진행하는
fit_transform()결과값을 반환합니다.
cmap = plt.get_cmap('rainbow', 10)
fig = plt.scatter(tsne_vector[:,0], tsne_vector[:,1], marker='.', c=train_Y[:5000], cmap=cmap)
cb = plt.colorbar(fig, ticks=range(10))
n_clusters = 10
tick_locs = (np.arange(n_clusters) + 0.5)*(n_clusters-1)/n_clusters
cb.set_ticks(tick_locs)
cb.set_ticklabels(range(10))
plt.show()

위 시각화 내용은 여기에서는 생략합니다.
- 출력 이미지의 클러스터링을 보면 이미지 라벨에 따라 같은 숫자끼리 비교적 잘 뭉쳐있는 것을 확인할 수 있습니다.
(6) t-SNE 결과 시각화
우선 코드를 작성하고, 결과물을 확인해봅니다.
%%time
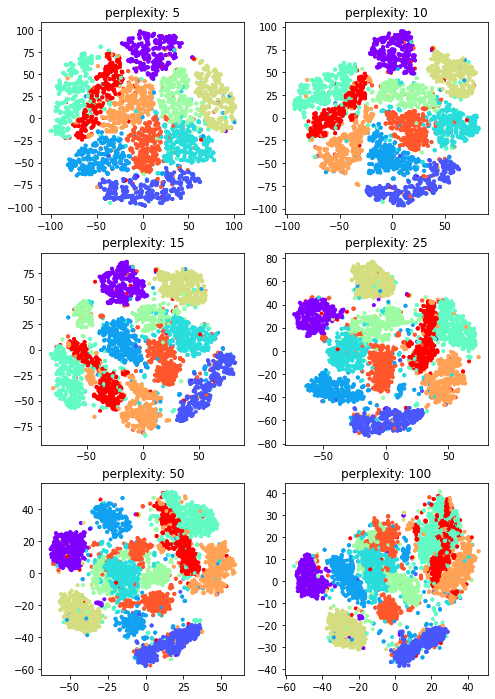
perplexities = [5, 10, 15, 25, 50, 100]
plt.figure(figsize=(8,12))
for c in range(6):
tsne = TSNE(n_components=2, learning_rate=100, perplexity=perplexities[c], random_state=0)
tsne_vector = tsne.fit_transform(latent_vector[:5000])
plt.subplot(3, 2, c+1)
plt.scatter(tsne_vector[:,0], tsne_vector[:,1], marker='.', c=train_Y[:5000], cmap='rainbow')
plt.title('perplexity: {0}'.format(perplexities[c]))
plt.show()
CPU times: user 7min 18s, sys: 1.17 s, total: 7min 19s
Wall time: 3min 52s
perplexity가 높아질수록 뭉치는 클러스터도 있지만, 뒤섞이는 클러스터도 보이는 것으로 볼 때 최적의 값을 찾기 위해서는 다른 하이퍼파라미터처럼 여러번의 실험이 필요한 것 같습니다.
(7) t-SNE 클러스터 위에 MNIST 이미지 표시
클러스터 분리 결과를 좀 더 직관적으로 확인하기 위해 t-SNE로 분리된 클러스터 위에 MNIST이미지를 표시합니다.
from matplotlib.offsetbox import TextArea, DrawingArea, OffsetImage, AnnotationBbox
plt.figure(figsize=(16, 16))
tsne=TSNE(n_components=2, learning_rate=100, perplexity=15, random_state=0)
tsne_vector=tsne.fit_transform(latent_vector[:5000])
ax = plt.subplot(1, 1, 1)
ax.scatter(tsne_vector[:, 0], tsne_vector[:,1], marker='.', c=train_Y[:5000], cmap='rainbow')
for i in range(200):
imagebox = OffsetImage(train_X[i].reshape(28, 28))
ab = AnnotationBbox(imagebox, (tsne_vector[i, 0], tsne_vector[i, 1]), frameon=False, pad=0.0)
ax.add_artist(ab)
ax.set_xticks([])
ax.set_yticks([])
plt.show()

전체적인 분포와 이미지를 같이 확인하기 위해 이미지는 200개만 표시합니다. 출력 이미지에서도 각 숫자는 대부분 자신이 속한 클러스터에 표시되고 있습니다.
t-SNE 시각화 위해 데이터를 표시하면 오토인코더로 추출된 잠재변수가 데이터를 효율적으로 압축하고 있음을 알 수 있습니다.
III. 연습 파일
VI. Reference
김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.
