Tensorflow 2.0 Tutorial ch7.1 - RNN 이론 (2)
공지
-
본 Tutorial은 교재
시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다. -
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶으신 분은 반드시 교재를 구매하실 것을 권해드립니다.

- 본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.
Tutorial
이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.
- Google Colab Tensorflow 2.0 Installation
- Tensorflow 2.0 Tutorial ch3.3.1 - 난수 생성 및 시그모이드 함수
- Tensorflow 2.0 Tutorial ch3.3.2 - 난수 생성 및 시그모이드 함수 편향성
- Tensorflow 2.0 Tutorial ch3.3.3 - 첫번째 신경망 네트워크 - AND
- Tensorflow 2.0 Tutorial ch3.3.4 - 두번째 신경망 네트워크 - OR
- Tensorflow 2.0 Tutorial ch3.3.5 - 세번째 신경망 네트워크 - XOR
- Tensorflow 2.0 Tutorial ch4.1 - 선형회귀
- Tensorflow 2.0 Tutorial ch4.2 - 다항회귀
- Tensorflow 2.0 Tutorial ch4.3 - 딥러닝 네트워크를 이용한 회귀
- Tensorflow 2.0 Tutorial ch4.4 - 보스턴 주택 가격 데이터세트
- Tensorflow 2.0 Tutorial ch5.1 - 분류
- Tensorflow 2.0 Tutorial ch5.2 - 다항분류
- Tensorflow 2.0 Tutorial ch5.3 - Fashion MNIST
- Tensorflow 2.0 Tutorial ch6.1-2 - CNN 이론
- Tensorflow 2.0 Tutorial ch6.3 - Fashion MNIST with CNN 실습
- Tensorflow 2.0 Tutorial ch6.4 - 모형의 성능 높이기
- Tensorflow 2.0 Tutorial ch7.1 - RNN 이론 (1)
I. 개요
GRU(Gated Recurrent Unit)레이어는 LSTM레이어와 비슷한 역할을 하지만 구조가 더 간단하기 때문에 계산상의 이점이 있고, 어떤 문제에서는 LSTM 레이어보다 좋은 성능을 보여주기도 합니다.12 셀로 나타낸 GRU 레이어의 계산 흐름은 LSTM과 비슷하지만, 조금 축약된 모습을 보입니다.3

자세한 수식 및 이론 설명은 교재를 구매하셔서 194-5페이지를 참고하시기를 바랍니다. GRU의 성능이 LSTM보다 실제로 성능이 좋은지, 수식이 줄었기 때문에, 또한 연산속도는 빨라졌는지 확인해보도록 합니다.
II. GRU 모델 정의 및 구현
ch7.1 - RNN(1) 이론에서 배웠던 곱셈 정의 문제를 다시 풀어보도록 합니다.
# 텐서플로 2 버전 선택
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import numpy as np
X = []
Y = []
for i in range(3000):
# 0 ~ 1 범위의 랜덤한 숫자 100개를 만듭니다.
lst = np.random.rand(100)
# 마킹할 숫자 2개의 인덱스를 뽑습니다.
idx = np.random.choice(100, 2, replace=False)
# 마킹 인덱스가 저장된 원-핫 인코딩 벡터를 만듭니다.
zeros=np.zeros(100)
zeros[idx]=1
# 마킹 인덱스와 랜덤한 숫자를 합쳐서 X에 저장합니다.
X.append(np.array(list(zip(zeros, lst))))
# 마킹 인덱스가 1인 값만 서로 곱해서 Y에 저장합니다.
Y.append(np.prod(lst[idx]))
model = tf.keras.Sequential([
tf.keras.layers.GRU(units=30, return_sequences=True, input_shape=[100,2]),
tf.keras.layers.GRU(units=30),
tf.keras.layers.Dense(1)
])
model.compile(optimizer='adam', loss='mse')
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru (GRU) (None, 100, 30) 3060
_________________________________________________________________
gru_1 (GRU) (None, 30) 5580
_________________________________________________________________
dense (Dense) (None, 1) 31
=================================================================
Total params: 8,671
Trainable params: 8,671
Non-trainable params: 0
_________________________________________________________________
기존 LSTM 모델 정의 코드에서 GRU로 바꿔서 간단히 모델을 정의할 수 있습니다. GRU레이어를 사용한 네트워크의 파라미터 수는 LSTM레이어의 파라미터 수보다 적습니다.
이전 포스트에서 작성했던 파라미터 수를 비교하면 다음과 같습니다.
| SimpleRNN | LSTM | GRU |
|---|---|---|
| 2,851 | 11,311 | 8,671 |
그럼 이제 실제로 학습시켜서 결과가 어떻게 나오는지 확인합니다. 코드 역시, 그 전과 큰 차이점은 없기 때문에 전체 소스코드를 이어서 작성합니다.
X = np.array(X)
Y = np.array(Y)
# 모형 학습
history = model.fit(X[:2560], Y[:2560], epochs=100, validation_split=0.2)
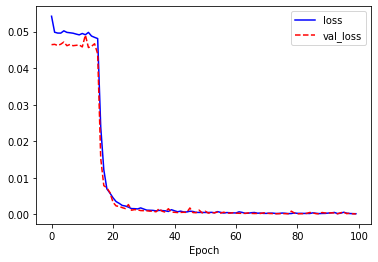
# 모형 학습 시각화
import matplotlib.pyplot as plt
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()
plt.show()
# 모형 테스트 및 결과
model.evaluate(X[2560:], Y[2560:])
prediction=model.predict(X[2560:2560+5])
# 5개 테스트 데이터에 대한 예측을 표시합니다.
for i in range(5):
print(Y[2560+i], '\t', prediction[i][0], '\tdiff:', abs(prediction[i][0] - Y[2560+i]))
prediction = model.predict(X[2560:])
fail = 0
for i in range(len(prediction)):
# 오차가 0.04 이상이면 오답입니다.
if abs(prediction[i][0] - Y[2560+i]) > 0.04:
fail +=1
print('correctness:', (440-fail)/440*100, '%')
Epoch 1/100
64/64 [==============================] - 1s 19ms/step - loss: 0.0542 - val_loss: 0.0464
Epoch 2/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0498 - val_loss: 0.0465
Epoch 3/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0496 - val_loss: 0.0462
Epoch 4/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0496 - val_loss: 0.0466
Epoch 5/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0502 - val_loss: 0.0472
Epoch 6/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0498 - val_loss: 0.0462
Epoch 7/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0497 - val_loss: 0.0465
Epoch 8/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0496 - val_loss: 0.0462
Epoch 9/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0493 - val_loss: 0.0463
Epoch 10/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0491 - val_loss: 0.0464
Epoch 11/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0495 - val_loss: 0.0458
Epoch 12/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0492 - val_loss: 0.0491
Epoch 13/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0498 - val_loss: 0.0457
Epoch 14/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0488 - val_loss: 0.0460
Epoch 15/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0484 - val_loss: 0.0467
Epoch 16/100
64/64 [==============================] - 1s 11ms/step - loss: 0.0481 - val_loss: 0.0439
Epoch 17/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0239 - val_loss: 0.0153
Epoch 18/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0122 - val_loss: 0.0079
Epoch 19/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0070 - val_loss: 0.0072
Epoch 20/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0058 - val_loss: 0.0060
Epoch 21/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0045 - val_loss: 0.0033
Epoch 22/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0035 - val_loss: 0.0023
Epoch 23/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0030 - val_loss: 0.0022
Epoch 24/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0024 - val_loss: 0.0018
Epoch 25/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0023 - val_loss: 0.0016
Epoch 26/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0020 - val_loss: 0.0027
Epoch 27/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0016 - val_loss: 0.0011
Epoch 28/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0016 - val_loss: 0.0013
Epoch 29/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0015 - val_loss: 0.0012
Epoch 30/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0018 - val_loss: 0.0010
Epoch 31/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0014 - val_loss: 0.0010
Epoch 32/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0011 - val_loss: 9.6678e-04
Epoch 33/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0011 - val_loss: 8.7013e-04
Epoch 34/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0011 - val_loss: 8.7790e-04
Epoch 35/100
64/64 [==============================] - 1s 10ms/step - loss: 9.3853e-04 - val_loss: 6.9370e-04
Epoch 36/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0011 - val_loss: 0.0016
Epoch 37/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0010 - val_loss: 8.4368e-04
Epoch 38/100
64/64 [==============================] - 1s 10ms/step - loss: 9.6391e-04 - val_loss: 6.0684e-04
Epoch 39/100
64/64 [==============================] - 1s 10ms/step - loss: 7.8758e-04 - val_loss: 0.0015
Epoch 40/100
64/64 [==============================] - 1s 10ms/step - loss: 0.0013 - val_loss: 6.3157e-04
Epoch 41/100
64/64 [==============================] - 1s 10ms/step - loss: 9.7273e-04 - val_loss: 5.5738e-04
Epoch 42/100
64/64 [==============================] - 1s 10ms/step - loss: 7.0651e-04 - val_loss: 4.9343e-04
Epoch 43/100
64/64 [==============================] - 1s 10ms/step - loss: 8.7092e-04 - val_loss: 5.3667e-04
Epoch 44/100
64/64 [==============================] - 1s 10ms/step - loss: 6.4929e-04 - val_loss: 5.6655e-04
Epoch 45/100
64/64 [==============================] - 1s 10ms/step - loss: 6.5691e-04 - val_loss: 5.3359e-04
Epoch 46/100
64/64 [==============================] - 1s 10ms/step - loss: 8.4880e-04 - val_loss: 0.0017
Epoch 47/100
64/64 [==============================] - 1s 11ms/step - loss: 7.9048e-04 - val_loss: 4.8470e-04
Epoch 48/100
64/64 [==============================] - 1s 10ms/step - loss: 5.2750e-04 - val_loss: 4.5355e-04
Epoch 49/100
64/64 [==============================] - 1s 10ms/step - loss: 5.2346e-04 - val_loss: 0.0011
Epoch 50/100
64/64 [==============================] - 1s 11ms/step - loss: 5.2244e-04 - val_loss: 3.9339e-04
Epoch 51/100
64/64 [==============================] - 1s 11ms/step - loss: 5.1538e-04 - val_loss: 8.5248e-04
Epoch 52/100
64/64 [==============================] - 1s 10ms/step - loss: 5.0478e-04 - val_loss: 3.3874e-04
Epoch 53/100
64/64 [==============================] - 1s 10ms/step - loss: 5.4496e-04 - val_loss: 5.0151e-04
Epoch 54/100
64/64 [==============================] - 1s 10ms/step - loss: 4.3863e-04 - val_loss: 4.1039e-04
Epoch 55/100
64/64 [==============================] - 1s 10ms/step - loss: 7.4540e-04 - val_loss: 6.3658e-04
Epoch 56/100
64/64 [==============================] - 1s 10ms/step - loss: 5.3960e-04 - val_loss: 3.4416e-04
Epoch 57/100
64/64 [==============================] - 1s 11ms/step - loss: 3.6213e-04 - val_loss: 5.8370e-04
Epoch 58/100
64/64 [==============================] - 1s 10ms/step - loss: 4.8387e-04 - val_loss: 3.6832e-04
Epoch 59/100
64/64 [==============================] - 1s 10ms/step - loss: 4.4107e-04 - val_loss: 3.1697e-04
Epoch 60/100
64/64 [==============================] - 1s 11ms/step - loss: 3.9765e-04 - val_loss: 4.5374e-04
Epoch 61/100
64/64 [==============================] - 1s 11ms/step - loss: 3.8165e-04 - val_loss: 3.2876e-04
Epoch 62/100
64/64 [==============================] - 1s 10ms/step - loss: 6.8677e-04 - val_loss: 2.9420e-04
Epoch 63/100
64/64 [==============================] - 1s 10ms/step - loss: 5.2809e-04 - val_loss: 2.7272e-04
Epoch 64/100
64/64 [==============================] - 1s 10ms/step - loss: 2.7761e-04 - val_loss: 2.6852e-04
Epoch 65/100
64/64 [==============================] - 1s 10ms/step - loss: 3.0836e-04 - val_loss: 4.0206e-04
Epoch 66/100
64/64 [==============================] - 1s 10ms/step - loss: 4.4454e-04 - val_loss: 2.6554e-04
Epoch 67/100
64/64 [==============================] - 1s 10ms/step - loss: 5.0457e-04 - val_loss: 2.2702e-04
Epoch 68/100
64/64 [==============================] - 1s 10ms/step - loss: 3.1455e-04 - val_loss: 2.5735e-04
Epoch 69/100
64/64 [==============================] - 1s 10ms/step - loss: 3.4775e-04 - val_loss: 2.4464e-04
Epoch 70/100
64/64 [==============================] - 1s 10ms/step - loss: 2.5858e-04 - val_loss: 4.1233e-04
Epoch 71/100
64/64 [==============================] - 1s 10ms/step - loss: 2.6686e-04 - val_loss: 3.1173e-04
Epoch 72/100
64/64 [==============================] - 1s 10ms/step - loss: 3.2840e-04 - val_loss: 2.2496e-04
Epoch 73/100
64/64 [==============================] - 1s 10ms/step - loss: 3.2419e-04 - val_loss: 2.0555e-04
Epoch 74/100
64/64 [==============================] - 1s 10ms/step - loss: 2.3337e-04 - val_loss: 1.6153e-04
Epoch 75/100
64/64 [==============================] - 1s 10ms/step - loss: 2.4482e-04 - val_loss: 1.9017e-04
Epoch 76/100
64/64 [==============================] - 1s 10ms/step - loss: 3.5401e-04 - val_loss: 2.0578e-04
Epoch 77/100
64/64 [==============================] - 1s 11ms/step - loss: 2.8999e-04 - val_loss: 1.8757e-04
Epoch 78/100
64/64 [==============================] - 1s 10ms/step - loss: 2.0261e-04 - val_loss: 1.6617e-04
Epoch 79/100
64/64 [==============================] - 1s 10ms/step - loss: 2.2359e-04 - val_loss: 8.6003e-04
Epoch 80/100
64/64 [==============================] - 1s 10ms/step - loss: 3.8440e-04 - val_loss: 3.4750e-04
Epoch 81/100
64/64 [==============================] - 1s 10ms/step - loss: 2.7182e-04 - val_loss: 1.4401e-04
Epoch 82/100
64/64 [==============================] - 1s 10ms/step - loss: 2.7468e-04 - val_loss: 1.6795e-04
Epoch 83/100
64/64 [==============================] - 1s 10ms/step - loss: 2.4761e-04 - val_loss: 1.9169e-04
Epoch 84/100
64/64 [==============================] - 1s 10ms/step - loss: 2.5236e-04 - val_loss: 2.6484e-04
Epoch 85/100
64/64 [==============================] - 1s 10ms/step - loss: 2.3328e-04 - val_loss: 5.1060e-04
Epoch 86/100
64/64 [==============================] - 1s 10ms/step - loss: 4.0916e-04 - val_loss: 4.0131e-04
Epoch 87/100
64/64 [==============================] - 1s 10ms/step - loss: 2.9090e-04 - val_loss: 1.8709e-04
Epoch 88/100
64/64 [==============================] - 1s 10ms/step - loss: 2.0704e-04 - val_loss: 1.4023e-04
Epoch 89/100
64/64 [==============================] - 1s 10ms/step - loss: 2.4698e-04 - val_loss: 5.0055e-04
Epoch 90/100
64/64 [==============================] - 1s 10ms/step - loss: 2.5488e-04 - val_loss: 3.7641e-04
Epoch 91/100
64/64 [==============================] - 1s 10ms/step - loss: 3.4907e-04 - val_loss: 3.2548e-04
Epoch 92/100
64/64 [==============================] - 1s 10ms/step - loss: 4.0255e-04 - val_loss: 4.1547e-04
Epoch 93/100
64/64 [==============================] - 1s 10ms/step - loss: 5.1706e-04 - val_loss: 3.9099e-04
Epoch 94/100
64/64 [==============================] - 1s 10ms/step - loss: 2.2027e-04 - val_loss: 1.5537e-04
Epoch 95/100
64/64 [==============================] - 1s 10ms/step - loss: 2.9934e-04 - val_loss: 4.1400e-04
Epoch 96/100
64/64 [==============================] - 1s 12ms/step - loss: 5.6970e-04 - val_loss: 6.6119e-04
Epoch 97/100
64/64 [==============================] - 1s 10ms/step - loss: 3.3246e-04 - val_loss: 1.8468e-04
Epoch 98/100
64/64 [==============================] - 1s 10ms/step - loss: 2.1950e-04 - val_loss: 2.9611e-04
Epoch 99/100
64/64 [==============================] - 1s 10ms/step - loss: 1.9392e-04 - val_loss: 1.4212e-04
Epoch 100/100
64/64 [==============================] - 1s 10ms/step - loss: 1.7158e-04 - val_loss: 1.1689e-04
14/14 [==============================] - 0s 5ms/step - loss: 1.3132e-04
0.03254906333292209 0.028674547 diff: 0.003874516703731644
0.0459566112724449 0.040693775 diff: 0.005262836453070817
0.5360537450610645 0.5460534 diff: 0.009999664515351503
0.14992662254277317 0.14886208 diff: 0.0010645437568768679
0.38647776052320765 0.38145044 diff: 0.005027316063292486
correctness: 99.31818181818181 %
정확도는 99.3%로 거의 99%에 가까운 값이 나옵니다. 이 문제에서는 LSTM 레이어보다 GRU레이어로 더 잘 풀리는 문제입니다.
마지막 이론으로 임베딩 레이어에 대해 배우도록 합니다.
III. 임베딩 레이어 기본 이론
임베딩 레이어(Embedding Layer)는 자연어를 수치화된 정보로 바꾸기 위한 레이어입니다. 자연어는 시간의 흐름에 따라 정보가 연속적으로 이어지는 시퀀스 데이터입니다. 이미지를 픽셀 단위로 잘게 쪼갤 수 있듯이 자연어도 정보를 잘게 쪼갤 수 있습니다. 영어는 문자(character), 한글은 문자를 넘어 자소 단위로도 쪼갤 수 있습니다. 과거에는 n-gram보다 단어나 문자 단위의 자연어 처리가 많이 쓰입니다.4
임베딩 레이어보다 좀 더 쉬운 기법은 자연어를 구성하는 단위에 대해 정수 인덱스(index)를 저장하는 방법입니다. 좀 더 쉽게 예로 들면, “This is a big cat"이라는 문장에 대해 정수 인덱스를 저장하면 처음 나오는 단어부터 인덱스를 저장합니다.
| 단어 | 인덱스 |
|---|---|
| this | 0 |
| is | 1 |
| a | 2 |
| big | 3 |
| cat | 4 |
이렇게 새로운 수치화된 데이터로 변환될 수 있습니다. 이 때 “This is big.“이라는 새로운 문장도 [0,1,3]이라는 데이터로 바뀔 수 있습니다. 이렇게 바뀐 데이터는 아래 그림과 같이 원-핫 인코딩을 이용해 단어의 인덱스에 해당하는 원소만 1이고 나머지는 0인 배열로 바뀝니다.
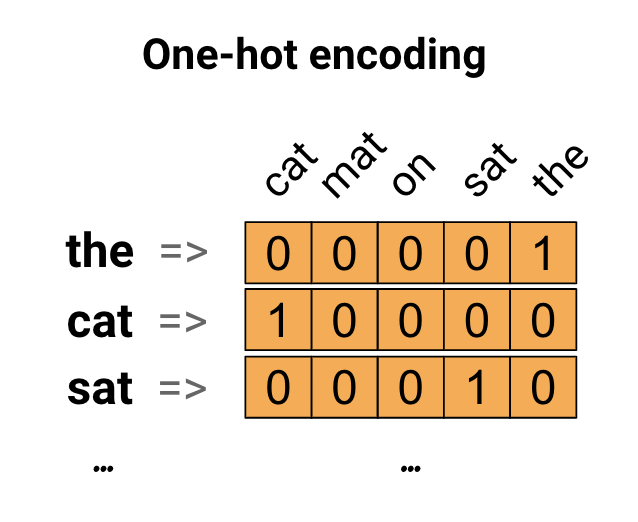
그런데, 인덱스를 사용할 때, 가장 큰 문제점은 사용하는 메모리의 양에 비해 너무 적은 정보량을 표현하는 것이고, 또 한가지 단점은 저장된 단어의 수가 많아질수록 원-핫 인코딩 배열의 두 번째 차원의 크기도 그에 비례해서 늘어나기 때문에 이 데이터가 차지하는 메모리의 양이 더욱 늘어나게 됩니다. 추가적인 이론에 대한 내용은 교재 201-3페이지를 확인하셔서 추가적인 이론 공부를 병행하는 것을 권합니다.
임베딩 레이어에 대해 학습시키는 방법은 Word2Vec, GloVe, FastText, ELMo등과 같은 방법론이 있습니다.
우선 단어 임베딩의 이론적인 코드 부분을 학습하고자 예제(감성분석)를 준비했습니다. 교재에는 조금 부족한 부분이라 판단되어, 텐서플로 공식홈페이지의 내용을 번역 및 축약합니다.5
(1) 코드 작성 및 설명
먼저 관련 모듈과 데이터를 가져옵니다.
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import tensorflow_datasets as tfds
tfds.disable_progress_bar()
# 데이터 수집 / 영화 데이터
dataset, info = tfds.load('imdb_reviews/subwords8k', with_info=True,
as_supervised=True)
train_examples, test_examples = dataset['train'], dataset['test']
[1mDownloading and preparing dataset imdb_reviews/subwords8k/1.0.0 (download: 80.23 MiB, generated: Unknown size, total: 80.23 MiB) to /root/tensorflow_datasets/imdb_reviews/subwords8k/1.0.0...[0m
Shuffling and writing examples to /root/tensorflow_datasets/imdb_reviews/subwords8k/1.0.0.incomplete70Q64U/imdb_reviews-train.tfrecord
Shuffling and writing examples to /root/tensorflow_datasets/imdb_reviews/subwords8k/1.0.0.incomplete70Q64U/imdb_reviews-test.tfrecord
Shuffling and writing examples to /root/tensorflow_datasets/imdb_reviews/subwords8k/1.0.0.incomplete70Q64U/imdb_reviews-unsupervised.tfrecord
[1mDataset imdb_reviews downloaded and prepared to /root/tensorflow_datasets/imdb_reviews/subwords8k/1.0.0. Subsequent calls will reuse this data.[0m
그리고, encoder를 통해서 실제 텍스트의 단어의 크기를 확인합니다.
encoder = info.features['text'].encoder
print('Vocabulary size: {}'.format(encoder.vocab_size))
Vocabulary size: 8185
이론에서 배웠던, 입력된 Sample String에 대해 인코딩된 값을 인덱스로 반환합니다. 그리고, 원 문자열도 같이 반환되어 어떻게 변환되는지 확인할 수 있습니다.
sample_string = 'Hello dschloe.'
encoded_string = encoder.encode(sample_string)
print('Encoded string is {}'.format(encoded_string))
original_string = encoder.decode(encoded_string)
print('The original string: "{}"'.format(original_string))
Encoded string is [4025, 222, 6995, 1163, 6275, 8039, 7975]
The original string: "Hello dschloe."
이제 다시 인덱스로 출력하면 전체 vocab_size에서 샘플 문자열이 어떤식으로 구성이 되는지 확인할 수 있습니다.
assert original_string == sample_string
for index in encoded_string:
print('{} ----> {}'.format(index, encoder.decode([index])))
4025 ----> Hell
222 ----> o
6995 ----> Ch
1163 ----> lo
6275 ----> Eva
8039 ----> n
7975 ----> .
이제 모형을 위해 학습 데이터를 준비합니다.
BUFFER_SIZE = 10000
BATCH_SIZE = 64
train_dataset = (train_examples
.shuffle(BUFFER_SIZE)
.padded_batch(BATCH_SIZE, padded_shapes=([None],[])))
test_dataset = (test_examples
.padded_batch(BATCH_SIZE, padded_shapes=([None],[])))
그런데, 아래 코드에서 pad라는 개념이 보일겁니다. pad은 공백을 의미합니다. padding의 개념이 있는 것은, 자연어에는 미리 정해놓을 수 없을 정도로 많은 단어가 존재하기 때문에, 보통은 정수 인덱스로 저장하지 않는 단어에 대한 임베딩 값을 별도로 마련합니다. 즉, 임베딩 레이어의 행 수가 10,000이라면 9,999는 미리 지정된 단어의 개수이고, 나머지 1은 지정되지 않은 단어를 위한 값입니다. 이것이 padding의 개념입니다.
padded_batch의 함수를 사용함으로써, UNK값으로 0을 넣어줍니다. 실제로 padded_batch가 어떻게 구현이 되는지 확인해봅니다.
train_batch, train_labels = next(iter(train_dataset))
train_batch.numpy()
array([[ 62, 9, 41, ..., 0, 0, 0],
[ 134, 142, 7968, ..., 0, 0, 0],
[ 12, 6130, 7, ..., 0, 0, 0],
...,
[ 684, 807, 455, ..., 0, 0, 0],
[ 373, 6, 1, ..., 6, 1803, 7975],
[ 62, 9, 45, ..., 0, 0, 0]])
위 값에 0이 있는 것을 확인할 수 있습니다. padded_batch를 함으로써 일종의 길이의 정규화를 진행한다고 보면 됩니다.
아래 코드는 모델 정의 및 학습에 관한 내용입니다. 튜토리얼에서 반복적으로 나오는 코드이기 때문에 여기에서는 설명을 생략합니다.
model = tf.keras.Sequential([
tf.keras.layers.Embedding(encoder.vocab_size, 64),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1)
])
model.compile(loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(1e-4),
metrics=['accuracy'])
history = model.fit(train_dataset, epochs=10,
validation_data=test_dataset,
validation_steps=30)
Epoch 1/10
391/391 [==============================] - 44s 113ms/step - loss: 0.6474 - accuracy: 0.5586 - val_loss: 0.4672 - val_accuracy: 0.7865
Epoch 2/10
391/391 [==============================] - 44s 113ms/step - loss: 0.3531 - accuracy: 0.8537 - val_loss: 0.3419 - val_accuracy: 0.8589
Epoch 3/10
391/391 [==============================] - 45s 114ms/step - loss: 0.2525 - accuracy: 0.9042 - val_loss: 0.3268 - val_accuracy: 0.8651
Epoch 4/10
391/391 [==============================] - 45s 114ms/step - loss: 0.2089 - accuracy: 0.9218 - val_loss: 0.3332 - val_accuracy: 0.8656
Epoch 5/10
391/391 [==============================] - 45s 116ms/step - loss: 0.1824 - accuracy: 0.9350 - val_loss: 0.3999 - val_accuracy: 0.8130
Epoch 6/10
391/391 [==============================] - 45s 115ms/step - loss: 0.1625 - accuracy: 0.9419 - val_loss: 0.3684 - val_accuracy: 0.8661
Epoch 7/10
391/391 [==============================] - 45s 116ms/step - loss: 0.1455 - accuracy: 0.9504 - val_loss: 0.3698 - val_accuracy: 0.8630
Epoch 8/10
391/391 [==============================] - 45s 115ms/step - loss: 0.1342 - accuracy: 0.9538 - val_loss: 0.4048 - val_accuracy: 0.8594
Epoch 9/10
391/391 [==============================] - 45s 116ms/step - loss: 0.1222 - accuracy: 0.9594 - val_loss: 0.4135 - val_accuracy: 0.8599
Epoch 10/10
391/391 [==============================] - 44s 114ms/step - loss: 0.1397 - accuracy: 0.9510 - val_loss: 0.4372 - val_accuracy: 0.8542
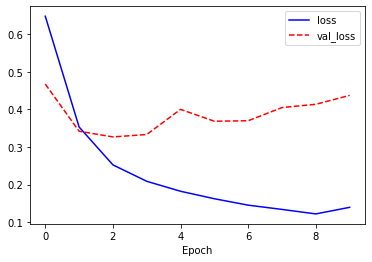
모형의 학습이 끝나면 실제로 잘 학습되는지 그래프를 작성합니다.
import matplotlib.pyplot as plt
history_dict = history.history
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()
plt.show()
test_loss, test_acc = model.evaluate(test_dataset)
print('Test Loss: {}'.format(test_loss))
print('Test Accuracy: {}'.format(test_acc))
391/391 [==============================] - 16s 42ms/step - loss: 0.4282 - accuracy: 0.8523
Test Loss: 0.4281919002532959
Test Accuracy: 0.8522800207138062
IV. 연습 파일
VI. Reference
김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.
-
Cho, K., Merrienboer, B. V., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). doi: 10.3115/v1/d14-1179 ↩︎
-
Chung, J., Gulcehre, C., Cho, K., & Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. In NIPS 2014 Workshop on Deep Learning, December 2014 ↩︎
-
교재 195페이지를 확인하면 여러 수식이 나옵니다. 여기서 주목해야 하는 것은
LSTM레이어보다 시그모이드 함수가 하나 적게 쓰였는데, 이것은 게이트의 수가 하나 줄어들었다는 것을 의미합니다. ↩︎ -
N-Gram은 간단하게 예를 들어 설명하면, “This is it"이라는 문장을 3개의 문자를 묶은
3-gram으로 나타내면 [“Thi”, “his”, “is “, “s i”, " is”, “is “, “s i”, " it”, “it."]이라는 배열로 나타낼 수 있습니다. ↩︎ -
Word embeddings, https://www.tensorflow.org/tutorials/text/word_embeddings ↩︎
