Tensorflow 2.0 Tutorial ch7.1 - RNN 이론 (1)

2020-04-22

Deep Learning, 딥러닝, 텐서플로 2.0, Python, Tensorflow 2.0, 텐서플로 2.0 튜토리얼, Tensorflow 2.0 Tutorial

Page content

공지

본 Tutorial은 교재 시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다.
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 반드시 교재를 구매하실 것을 권해드립니다.

본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.

Tutorial

이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.

I. 개요

순환 신경망(Recurrent Neural Network; RNN)은 지금까지 살펴본 네트워크와는 입력을 받아들이는 방식과 처리하는 방식에 약간 차이가 있습니다. 순환 신경망은 순서가 있는 데이터를 입력으로 받고, 같은 네트워크를 이용해 변화하는 입력에 대한 출력을 얻어냅니다.

순서가 있는 데이터는 음악, 자연어, 날씨, 주가 등 시간의 흐름에 따라 변화하고 그 변화가 의미를 갖는 데이터입니다.

II. 순환 신경망의 구조

우선 CNN과 RNN의 딥러닝 구조의 차이점에 대해 이미지¹로 확인하면 보다 직관적으로 이해가 될 수 있습니다.

CNN의 구조는 본 교재를 계속 따라오셨다면 익숙하다시피, 아래와 같은 구조로 되어 있습니다.

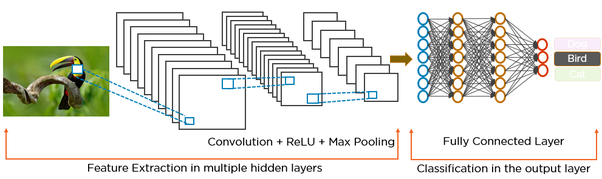
그러나, RNN의 구조는 아래에서 확인할 수 있는 것처럼, 순환 모양의 화살표가 있다는 것이 차이점입니다.

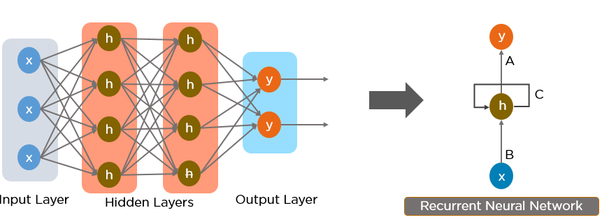
순환 신경망의 특징에 대해 간단하게 요약하면 다음과 같습니다.

입력 X를 받아서, 출력 Y를 반환합니다.
순환구조를 가지고 있다; 어떤 레이어의 출력을 다시 입력으로 받는 구조를 말합니다.
순환 신경망은 입력과 출력의 길이에 제한이 없습니다.
순환 신경망은 이미지에 대한 설명을 생성하는 이미지 설명 생성, 문장의 긍정/부정을 판단하는 감성 분석, 하나의 언어를 다른 언어로 번역하는 기계 번역(Machine Translation) 등 다양한 용도로 활용됩니다.

순환 신경망의 이론에 대한 자세한 설명은 교재 (p. 174-5)를 참조하시기를 바랍니다.

III. 주요 레이어 정리

순환 신경망의 가장 기초적인 레이어는 SimpleRNN 레이어이며, 이 레이어에서 출발한 LSTM 레이어 또는 GRU레이어가 주로 쓰입니다. 그리고, 자연어 처리를 위해서 꼭 알아둬야 하는 임베딩(Embedding)레이어도 같이 알아봅니다.

(1) SimpleRNN 레이어

SimpleRNN레이어는 가장 간단한 형태의 RNN레이업니다. 수식에 대한 설명은 교재(p. 176)를 참고합니다. 이 때 주로 사용되는 활성화 함수로는 tanh가 사용됩니다. tanh는 실수 입력을 받아 -1에서 1사이의 출력 값을 반환하는 활성하 함수이며, 이 활성화 함수 자리에 ReLU같은 다른 활성화함수를 쓸 수도 있습니다.

SimpleRNN 레이어는 tf.keras에서 한 줄로 간단하게 생성이 가능합니다.

rnn1 = tf.keras.layers.SimpleRNN(units=1, activation='tanh', return_sequences=True)

units는 SimpleRNN의 레이어에 존재하는 뉴런의 수를 의미합니다. return_sequences는 출력으로 시퀀스 전체를 출력할지 여부를 나타내는 옵션이며, 여러 개의 RNN 레이어를 쌓을 때 쓰입니다.

간단한 예제를 통해서 학습을 해봅니다.

# 텐서플로 2 버전 선택
try:
    # %tensorflow_version only exists in Colab.
    %tensorflow_version 2.x
except Exception:
    pass
import tensorflow as tf
import numpy as np

X = []
Y = []

for i in range(6):
  # [0, 1, 2, 3], [1, 2, 3, 4]
  lst = list(range(i,i+4))

  # 위에서 구한 시퀀스의 숫자들을 각각 10으로 나눈 다음 저장합니다. 
  # SimpleRNN에 각 타임스텝에 하나씩 숫자가 들어가기 때문에 여기서도 하나씩 분리해서 배열에 저장합니다. 
  X.append(list(map(lambda c:[c/10], lst)))

  # 정답에 해당하는 4, 5 등의 정수 역시 앞에서처럼 10으로 나눠서 저장합니다. 
  Y.append((i+4)/10)

X = np.array(X)
Y = np.array(Y)

for i in range(len(X)): 
  print(X[i], Y[i])

[[0. ]
 [0.1]
 [0.2]
 [0.3]] 0.4
[[0.1]
 [0.2]
 [0.3]
 [0.4]] 0.5
[[0.2]
 [0.3]
 [0.4]
 [0.5]] 0.6
[[0.3]
 [0.4]
 [0.5]
 [0.6]] 0.7
[[0.4]
 [0.5]
 [0.6]
 [0.7]] 0.8
[[0.5]
 [0.6]
 [0.7]
 [0.8]] 0.9

이제 SimpleRNN 레이어를 사용한 네트워크를 정의합니다. 모델 구조는 지금까지 계속 봐온 시퀀셜 모델이고, 출력을 위한 Dense 레이어가 뒤에 추가되어 있습니다.

# 7.3 시퀀스 예측 모델 정의
model = tf.keras.Sequential([
    tf.keras.layers.SimpleRNN(units=10, return_sequences=False, input_shape=[4,1]),
    tf.keras.layers.Dense(1)
])

model.compile(optimizer='adam', loss='mse')
model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
simple_rnn_1 (SimpleRNN)     (None, 10)                120       
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 11        
=================================================================
Total params: 131
Trainable params: 131
Non-trainable params: 0
_________________________________________________________________

여기에서 주목해야 하는 코드는 input_shape입니다. 여기에서 [4,1]은 각각 timesteps, input_dim을 나타냅니다. 타입스텝은(timesteps)이란 순환 신경망이 입력에 대해 계산을 반복하는 횟수를 말하고, input_dim은 벡터의 크기를 나타냅니다.

[[0. ]
 [0.1]
 [0.2]
 [0.3]] 0.4

두번째의 4는 타임스텝, 세번째의 1은 input_dim이 됩니다. 그림을 참조하면 훨씬 이해하기 쉽습니다. (교재, p.180)

시퀀스 예측 모델은 4 타임스텝에 걸쳐 입력을 받고, 마지막에 출력값을 다음 레이어로 반환합니다. 우리가 추가한 Dense레이어에는 별도의 활성화함수가 없기 때문에 $h_{3}$는 바로 $y_{3}$이 됩니다. 그리고 이 값과 0.4와의 차이가 mse, 즉 평균 제곱 오차(Mean Squared Error)가 됩니다.

이제 훈련을 시킵니다. 이 때, verbose값을 0으로 놓으면 훈련 과정에서의 출력이 나오지 않습니다.

model.fit(X, Y, epochs=100, verbose=0)
print(model.predict(X))

[[0.37582147]
 [0.5110225 ]
 [0.6267948 ]
 [0.72202194]
 [0.7992587 ]
 [0.86209536]]

X가 주어졌을 때 학습된 모델이 시퀀스를 어떻게 예측하는지 확인해보면 얼추 비슷하게 예측하고 있음을 확인할 수 있습니다. 그렇다면 학습과정에서 본 적이 없는 테스트 데이터를 넣으면 어떨까요? X의 범위가 0.0~0.9 였으니, 양쪽으로 한 칸씩 더 나간 데이터를 입력합니다.

print(model.predict(np.array([[[0.6], [0.7], [0.8], [0.9]]])))
print(model.predict(np.array([[[-0.1], [0.0], [0.1], [0.2]]])))

[[0.9137889]]
[[0.22816285]]

1을 예측하기를 원한 데이터의 출력으로는 0.91을 0.3을 예측하기 원한 데이터의 출력으로는 0.22의 값을 반환했습니다.

실무에서는 SimpleRNN보다는 LSTM 레이어와 GRU레이어를 사용합니다.

(2) LSTM 레이어

SimpleRNN 레이어에는 한 가지 치명적인 단점이 존재합니다. 입력 데이터가 길어질수록, 즉 데이터의 타임스텝이 길어질수록 학습 능력이 떨어진다는 점입니다. 이를 장기의존성(Long-Term Dependency)문제라고 하며, 입력 데이터와 출력 사이의 길이가 멀어질수록 연관 관계가 적어집니다.

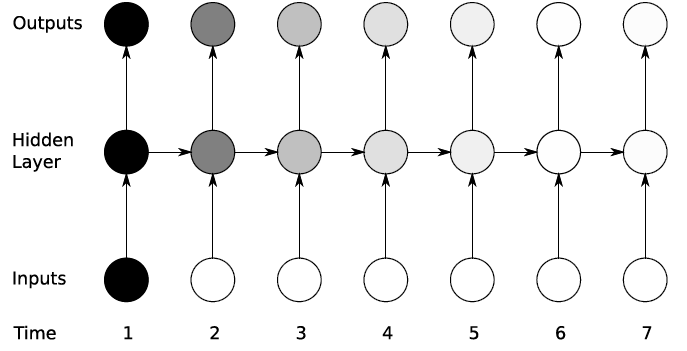
위 그림이 이러한 문제를 적절하게 표현한 것입니다. 입력 데이터가 길어지면 길어질수록 출력값의 연관 관계가 적어지는 것을 볼 수 있습니다.

이러한 문제점을 해결하기 위해 LSTM이 제안 되었습니다.² 셀로 나타낸 SimpleRNN과 LSTM의 계산 흐름을 보면 조금 이해가 될 것입니다.

먼저 SimpleRNN의 그림은 아래와 같습니다.

여기에서는 타임스텝의 방향으로 $h_{t}$만 전달되고 있음을 확인할 수 있습니다.

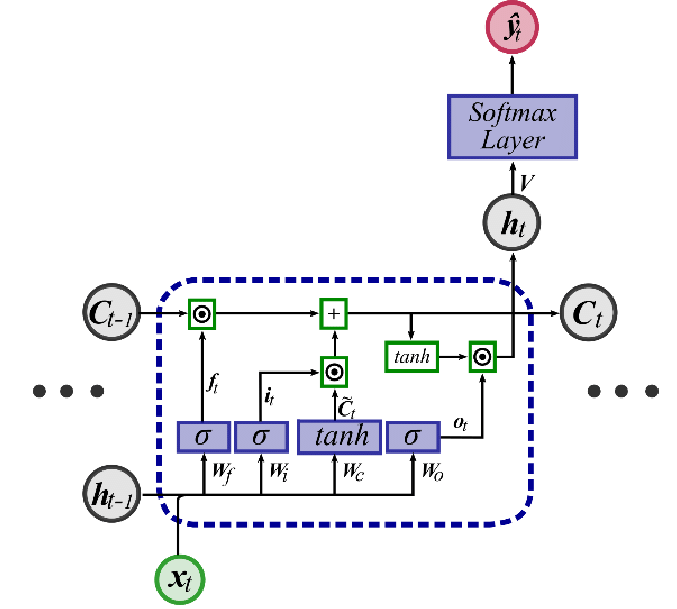
그런데, 여기에서는 셀 상테인 $c_{t}$가 평생선을 그리며 함께 전달되고 있습니다. 이처럼 타임스텝을 가로지르며 LSTM 셀 상태가 보존되기 때문에 장기의존성 문제를 해결할 수 있다는 것이 LSTM의 핵심 아이디어입니다.

교재 184페이지를 보면 위 셀에 대한 수식이 존재합니다만, 수식에 대한 구체적인 이해가 자료가 필요하다면 크리스토퍼 올라(Christopher Olah)의 블로그 글을 참고합니다.³

LSTM의 학습 능력을 확인하기 위한 예제는 LSTM을 처음 제안한 논문에 나온 실험 여섯개 중 다섯 번째인 곱셈 문제(Multiplication Problem)입니다. 이 문제는 말 그대로 실수에 대해 곱셈을 하는 문제인데, 고려해야 할 실수의 범위가 100개이고 그 중에서 마킹된 두개의 숫자만 곱해야 한다는 특이한 문제입니다.

# 텐서플로 2 버전 선택
try:
    # %tensorflow_version only exists in Colab.
    %tensorflow_version 2.x
except Exception:
    pass
import tensorflow as tf
import numpy as np

X = []
Y = []
for i in range(3000): 
  # 0 ~ 1 범위의 랜덤한 숫자 100개를 만듭니다. 
  lst = np.random.rand(100)

  # 마킹할 숫자 2개의 인덱스를 뽑습니다. 
  idx = np.random.choice(100, 2, replace=False)

  # 마킹 인덱스가 저장된 원-핫 인코딩 벡터를 만듭니다. 
  zeros=np.zeros(100)
  zeros[idx]=1
  
  # 마킹 인덱스와 랜덤한 숫자를 합쳐서 X에 저장합니다. 
  X.append(np.array(list(zip(zeros, lst))))
  # 마킹 인덱스가 1인 값만 서로 곱해서 Y에 저장합니다. 
  Y.append(np.prod(lst[idx]))

print(X[0], Y[0])

[[0.         0.56858055]
..
 [0.         0.12100308]
 [1.         0.14539513]
 [0.         0.43342875]
..
 [0.         0.5772363 ]
 [1.         0.21461413]
 [0.         0.95933064]
..
 [0.         0.55055634]
 [0.         0.20978592]] 0.03120384949137252

입력된 값이 길지만, 1은 두번만 들어가 있기 때문에, 1이 찍인 원소를 찾습니다. [1. 0.08361932]과 [1. 0.66439549]이 확인이 됩니다.

0.08361932와 0.66439549를 곱하면 0.055556298045436값이 나옵니다. SimpleRNN 레이어를 이용한 곱셈 문제 모델을 정의합니다.

model = tf.keras.Sequential([
  tf.keras.layers.SimpleRNN(units=30, return_sequences=True, input_shape=[100,2]), 
  tf.keras.layers.SimpleRNN(units=30), 
  tf.keras.layers.Dense(1)
])

model.compile(optimizer='adam', loss='mse')
model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
simple_rnn (SimpleRNN)       (None, 100, 30)           990       
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, 30)                1830      
_________________________________________________________________
dense (Dense)                (None, 1)                 31        
=================================================================
Total params: 2,851
Trainable params: 2,851
Non-trainable params: 0
_________________________________________________________________

RNN 레이어를 겹치기 위해 첫 번째 SimpleRNN레이어에서 return_sequences=True로 설정된 것을 확인할 수 있습니다. return_sequences는 레이어의 출력을 다음 레이어로 그대로 넘겨주게 됩니다.

겹치는 레이어의 구조에 대한 이론 설명은 교재 188페이지를 참조하시기를 바랍니다. RNN은 CNN보다 학습 시간이 오래 걸리는 편이기 때문에 반드시 가속기를 GPU로 바꿔줍니다.

X = np.array(X)
Y = np.array(Y)

# 2560개의 데이터만 학습시킵니다. 검증 데이터는 20%로 저장합니다. 
history=model.fit(X[:2560], Y[:2560], epochs=100, validation_split=0.2)

Epoch 1/100
64/64 [==============================] - 8s 118ms/step - loss: 0.0559 - val_loss: 0.0494
Epoch 2/100
64/64 [==============================] - 8s 119ms/step - loss: 0.0493 - val_loss: 0.0480
Epoch 3/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0480 - val_loss: 0.0479
Epoch 4/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0487 - val_loss: 0.0471
Epoch 5/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0478 - val_loss: 0.0539
Epoch 6/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0477 - val_loss: 0.0518
Epoch 7/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0481 - val_loss: 0.0473
Epoch 8/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0472 - val_loss: 0.0490
Epoch 9/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0468 - val_loss: 0.0486
Epoch 10/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0464 - val_loss: 0.0507
Epoch 11/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0482 - val_loss: 0.0481
Epoch 12/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0481 - val_loss: 0.0488
Epoch 13/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0475 - val_loss: 0.0491
Epoch 14/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0468 - val_loss: 0.0473
Epoch 15/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0464 - val_loss: 0.0496
Epoch 16/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0474 - val_loss: 0.0493
Epoch 17/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0458 - val_loss: 0.0495
Epoch 18/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0458 - val_loss: 0.0495
Epoch 19/100
64/64 [==============================] - 7s 111ms/step - loss: 0.0452 - val_loss: 0.0487
Epoch 20/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0456 - val_loss: 0.0505
Epoch 21/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0449 - val_loss: 0.0490
Epoch 22/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0447 - val_loss: 0.0475
Epoch 23/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0444 - val_loss: 0.0494
Epoch 24/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0456 - val_loss: 0.0492
Epoch 25/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0446 - val_loss: 0.0501
Epoch 26/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0450 - val_loss: 0.0508
Epoch 27/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0442 - val_loss: 0.0519
Epoch 28/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0433 - val_loss: 0.0489
Epoch 29/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0436 - val_loss: 0.0497
Epoch 30/100
64/64 [==============================] - 8s 118ms/step - loss: 0.0441 - val_loss: 0.0519
Epoch 31/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0442 - val_loss: 0.0501
Epoch 32/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0422 - val_loss: 0.0488
Epoch 33/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0427 - val_loss: 0.0564
Epoch 34/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0429 - val_loss: 0.0511
Epoch 35/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0417 - val_loss: 0.0525
Epoch 36/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0411 - val_loss: 0.0520
Epoch 37/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0429 - val_loss: 0.0525
Epoch 38/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0412 - val_loss: 0.0502
Epoch 39/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0410 - val_loss: 0.0556
Epoch 40/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0407 - val_loss: 0.0520
Epoch 41/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0404 - val_loss: 0.0493
Epoch 42/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0388 - val_loss: 0.0541
Epoch 43/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0391 - val_loss: 0.0563
Epoch 44/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0392 - val_loss: 0.0506
Epoch 45/100
64/64 [==============================] - 7s 111ms/step - loss: 0.0400 - val_loss: 0.0556
Epoch 46/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0390 - val_loss: 0.0554
Epoch 47/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0385 - val_loss: 0.0515
Epoch 48/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0373 - val_loss: 0.0522
Epoch 49/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0373 - val_loss: 0.0556
Epoch 50/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0379 - val_loss: 0.0587
Epoch 51/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0371 - val_loss: 0.0550
Epoch 52/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0362 - val_loss: 0.0537
Epoch 53/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0364 - val_loss: 0.0591
Epoch 54/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0356 - val_loss: 0.0537
Epoch 55/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0348 - val_loss: 0.0591
Epoch 56/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0351 - val_loss: 0.0572
Epoch 57/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0339 - val_loss: 0.0585
Epoch 58/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0336 - val_loss: 0.0593
Epoch 59/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0337 - val_loss: 0.0587
Epoch 60/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0339 - val_loss: 0.0574
Epoch 61/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0323 - val_loss: 0.0582
Epoch 62/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0328 - val_loss: 0.0586
Epoch 63/100
64/64 [==============================] - 7s 112ms/step - loss: 0.0329 - val_loss: 0.0572
Epoch 64/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0318 - val_loss: 0.0610
Epoch 65/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0315 - val_loss: 0.0537
Epoch 66/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0309 - val_loss: 0.0599
Epoch 67/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0305 - val_loss: 0.0585
Epoch 68/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0303 - val_loss: 0.0599
Epoch 69/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0297 - val_loss: 0.0633
Epoch 70/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0296 - val_loss: 0.0600
Epoch 71/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0289 - val_loss: 0.0612
Epoch 72/100
64/64 [==============================] - 8s 120ms/step - loss: 0.0284 - val_loss: 0.0619
Epoch 73/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0287 - val_loss: 0.0637
Epoch 74/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0291 - val_loss: 0.0568
Epoch 75/100
64/64 [==============================] - 7s 111ms/step - loss: 0.0287 - val_loss: 0.0617
Epoch 76/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0287 - val_loss: 0.0605
Epoch 77/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0272 - val_loss: 0.0614
Epoch 78/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0269 - val_loss: 0.0606
Epoch 79/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0264 - val_loss: 0.0630
Epoch 80/100
64/64 [==============================] - 8s 117ms/step - loss: 0.0258 - val_loss: 0.0701
Epoch 81/100
64/64 [==============================] - 7s 117ms/step - loss: 0.0263 - val_loss: 0.0633
Epoch 82/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0267 - val_loss: 0.0635
Epoch 83/100
64/64 [==============================] - 7s 117ms/step - loss: 0.0261 - val_loss: 0.0666
Epoch 84/100
64/64 [==============================] - 8s 119ms/step - loss: 0.0254 - val_loss: 0.0624
Epoch 85/100
64/64 [==============================] - 8s 119ms/step - loss: 0.0253 - val_loss: 0.0601
Epoch 86/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0263 - val_loss: 0.0647
Epoch 87/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0238 - val_loss: 0.0676
Epoch 88/100
64/64 [==============================] - 7s 115ms/step - loss: 0.0239 - val_loss: 0.0661
Epoch 89/100
64/64 [==============================] - 8s 118ms/step - loss: 0.0237 - val_loss: 0.0641
Epoch 90/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0239 - val_loss: 0.0680
Epoch 91/100
64/64 [==============================] - 7s 116ms/step - loss: 0.0222 - val_loss: 0.0672
Epoch 92/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0230 - val_loss: 0.0659
Epoch 93/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0222 - val_loss: 0.0668
Epoch 94/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0235 - val_loss: 0.0634
Epoch 95/100
64/64 [==============================] - 7s 114ms/step - loss: 0.0231 - val_loss: 0.0660
Epoch 96/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0224 - val_loss: 0.0654
Epoch 97/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0211 - val_loss: 0.0657
Epoch 98/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0217 - val_loss: 0.0689
Epoch 99/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0212 - val_loss: 0.0667
Epoch 100/100
64/64 [==============================] - 7s 113ms/step - loss: 0.0216 - val_loss: 0.0664

훈련 데이터의 손실(loss)과 검증 데이터의 손실(var_loss)는 감소하지 않고 오히려 증가하는 것 같습니다. 경향을 직관적으로 파악하기 위해 history 변수에 저장된 값으로 그래프를 그려봅니다.

import matplotlib.pyplot as plt
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()
plt.show()

png

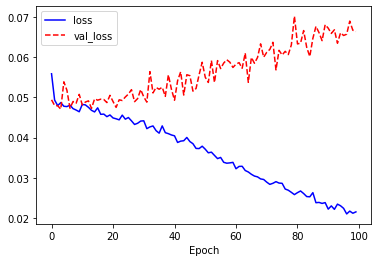
학습 결과는 전형적인 과적합 그래프를 보여줍니다. 테스트 데이터에 대한 예측은 어떨까요? 논문에서는 오차가 0.04 이상일 때 오답으로 처리합니다.

model.evaluate(X[2560:], Y[2560:])
prediction=model.predict(X[2560:2560+5])

# 5개 테스트 데이터에 대한 예측을 표시합니다. 
for i in range(5): 
  print(Y[2560+i], '\t', prediction[i][0], '\tdiff:', abs(prediction[i][0] - Y[2560+i]))

prediction = model.predict(X[2560:])
fail = 0
for i in range(len(prediction)):
  # 오차가 0.04 이상이면 오답입니다. 
  if abs(prediction[i][0] - Y[2560+i]) > 0.04:
    fail +=1

print('correctness:', (440-fail)/440*100, '%')

14/14 [==============================] - 0s 16ms/step - loss: 0.0667
0.009316712705671063 	 -0.05508966 	diff: 0.06440637269455123
0.1595728709352136 	 0.051416673 	diff: 0.10815619816900496
0.343633615267837 	 0.27744463 	diff: 0.06618898440655463
0.047836290850227836 	 0.23675384 	diff: 0.1889175454239192
0.07471709800989841 	 0.19511518 	diff: 0.12039808081357266
correctness: 12.727272727272727 %

먼저 전체에 대한 평가는 0.0667의 loss가 나왔습니다. 위에서 본 100번째의 에포크의 val_loss인 0.0664보다도 높은 값으로, 네트워크가 학습 과정에서 한번도 못 본 테스트 데이터에 대해서는 잘 예측하지 못합니다. 5개의 테스트 데이터에 대한 샘플은 오차가 0.01에서 0.18까지 다양하게 나타나며, 가장 중요한 정확도는 12.72로 확인 됩니다.

그렇다면 LSTM레이어는 어떨까요? 이 문제를 풀기 위해 시퀀셜 모델을 정의합니다.

model = tf.keras.Sequential([
  tf.keras.layers.LSTM(units=30, return_sequences=True, input_shape=[100,2]), 
  tf.keras.layers.LSTM(units=30), 
  tf.keras.layers.Dense(1)
])

model.compile(optimizer='adam', loss='mse')
model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm (LSTM)                  (None, 100, 30)           3960      
_________________________________________________________________
lstm_1 (LSTM)                (None, 30)                7320      
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 31        
=================================================================
Total params: 11,311
Trainable params: 11,311
Non-trainable params: 0
_________________________________________________________________

차이점은 SimpleRNN을 LSTM으로 바꾼 것 뿐입니다. 네트워크의 학습코드도 동일합니다.

X = np.array(X)
Y = np.array(Y)

# 2560개의 데이터만 학습시킵니다. 검증 데이터는 20%로 저장합니다. 
history=model.fit(X[:2560], Y[:2560], epochs=100, validation_split=0.2)

import matplotlib.pyplot as plt
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()
plt.show()

Epoch 1/100
64/64 [==============================] - 3s 54ms/step - loss: 0.0507 - val_loss: 0.0470
Epoch 2/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0472 - val_loss: 0.0469
Epoch 3/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0473 - val_loss: 0.0482
Epoch 4/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0474 - val_loss: 0.0482
Epoch 5/100
64/64 [==============================] - 3s 44ms/step - loss: 0.0474 - val_loss: 0.0471
Epoch 6/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0474 - val_loss: 0.0476
Epoch 7/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0471 - val_loss: 0.0474
Epoch 8/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0477 - val_loss: 0.0474
Epoch 9/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0472 - val_loss: 0.0472
Epoch 10/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0469 - val_loss: 0.0471
Epoch 11/100
64/64 [==============================] - 3s 44ms/step - loss: 0.0471 - val_loss: 0.0484
Epoch 12/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0473 - val_loss: 0.0472
Epoch 13/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0467 - val_loss: 0.0483
Epoch 14/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0466 - val_loss: 0.0471
Epoch 15/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0470 - val_loss: 0.0470
Epoch 16/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0466 - val_loss: 0.0471
Epoch 17/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0464 - val_loss: 0.0470
Epoch 18/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0464 - val_loss: 0.0483
Epoch 19/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0465 - val_loss: 0.0467
Epoch 20/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0462 - val_loss: 0.0465
Epoch 21/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0481 - val_loss: 0.0468
Epoch 22/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0467 - val_loss: 0.0474
Epoch 23/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0465 - val_loss: 0.0468
Epoch 24/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0463 - val_loss: 0.0471
Epoch 25/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0461 - val_loss: 0.0478
Epoch 26/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0457 - val_loss: 0.0464
Epoch 27/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0456 - val_loss: 0.0462
Epoch 28/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0459 - val_loss: 0.0485
Epoch 29/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0454 - val_loss: 0.0460
Epoch 30/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0474 - val_loss: 0.0464
Epoch 31/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0457 - val_loss: 0.0475
Epoch 32/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0455 - val_loss: 0.0461
Epoch 33/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0451 - val_loss: 0.0455
Epoch 34/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0448 - val_loss: 0.0450
Epoch 35/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0438 - val_loss: 0.0524
Epoch 36/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0453 - val_loss: 0.0448
Epoch 37/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0427 - val_loss: 0.0408
Epoch 38/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0481 - val_loss: 0.0462
Epoch 39/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0457 - val_loss: 0.0455
Epoch 40/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0447 - val_loss: 0.0443
Epoch 41/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0419 - val_loss: 0.0390
Epoch 42/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0353 - val_loss: 0.0254
Epoch 43/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0223 - val_loss: 0.0199
Epoch 44/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0188 - val_loss: 0.0155
Epoch 45/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0117 - val_loss: 0.0099
Epoch 46/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0092 - val_loss: 0.0070
Epoch 47/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0060 - val_loss: 0.0046
Epoch 48/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0062 - val_loss: 0.0043
Epoch 49/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0131 - val_loss: 0.0063
Epoch 50/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0050 - val_loss: 0.0041
Epoch 51/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0035 - val_loss: 0.0033
Epoch 52/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0032 - val_loss: 0.0034
Epoch 53/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0029 - val_loss: 0.0029
Epoch 54/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0033 - val_loss: 0.0024
Epoch 55/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0034 - val_loss: 0.0025
Epoch 56/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0026 - val_loss: 0.0031
Epoch 57/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0023 - val_loss: 0.0023
Epoch 58/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0022 - val_loss: 0.0020
Epoch 59/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0017 - val_loss: 0.0023
Epoch 60/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0018 - val_loss: 0.0032
Epoch 61/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0024 - val_loss: 0.0017
Epoch 62/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0018 - val_loss: 0.0040
Epoch 63/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0018 - val_loss: 0.0015
Epoch 64/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0018 - val_loss: 0.0016
Epoch 65/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0013 - val_loss: 0.0017
Epoch 66/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0012 - val_loss: 0.0017
Epoch 67/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0016 - val_loss: 0.0021
Epoch 68/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0013 - val_loss: 0.0015
Epoch 69/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0011 - val_loss: 0.0010
Epoch 70/100
64/64 [==============================] - 3s 42ms/step - loss: 8.9019e-04 - val_loss: 0.0012
Epoch 71/100
64/64 [==============================] - 3s 43ms/step - loss: 9.5466e-04 - val_loss: 9.1598e-04
Epoch 72/100
64/64 [==============================] - 3s 43ms/step - loss: 0.0012 - val_loss: 0.0013
Epoch 73/100
64/64 [==============================] - 3s 42ms/step - loss: 9.1245e-04 - val_loss: 9.0190e-04
Epoch 74/100
64/64 [==============================] - 3s 43ms/step - loss: 7.8530e-04 - val_loss: 8.0207e-04
Epoch 75/100
64/64 [==============================] - 3s 42ms/step - loss: 9.1405e-04 - val_loss: 8.6976e-04
Epoch 76/100
64/64 [==============================] - 3s 42ms/step - loss: 8.3703e-04 - val_loss: 8.9048e-04
Epoch 77/100
64/64 [==============================] - 3s 42ms/step - loss: 7.5276e-04 - val_loss: 8.5232e-04
Epoch 78/100
64/64 [==============================] - 3s 42ms/step - loss: 7.6209e-04 - val_loss: 8.4933e-04
Epoch 79/100
64/64 [==============================] - 3s 42ms/step - loss: 6.7965e-04 - val_loss: 6.3633e-04
Epoch 80/100
64/64 [==============================] - 3s 43ms/step - loss: 7.7308e-04 - val_loss: 6.0886e-04
Epoch 81/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0020 - val_loss: 7.1028e-04
Epoch 82/100
64/64 [==============================] - 3s 42ms/step - loss: 5.6736e-04 - val_loss: 6.5136e-04
Epoch 83/100
64/64 [==============================] - 3s 42ms/step - loss: 0.0012 - val_loss: 0.0010
Epoch 84/100
64/64 [==============================] - 3s 43ms/step - loss: 5.5983e-04 - val_loss: 6.3431e-04
Epoch 85/100
64/64 [==============================] - 3s 42ms/step - loss: 5.7588e-04 - val_loss: 6.2150e-04
Epoch 86/100
64/64 [==============================] - 3s 43ms/step - loss: 5.1412e-04 - val_loss: 4.9473e-04
Epoch 87/100
64/64 [==============================] - 3s 42ms/step - loss: 4.5491e-04 - val_loss: 6.0971e-04
Epoch 88/100
64/64 [==============================] - 3s 42ms/step - loss: 5.9710e-04 - val_loss: 5.0932e-04
Epoch 89/100
64/64 [==============================] - 3s 43ms/step - loss: 3.7854e-04 - val_loss: 7.4333e-04
Epoch 90/100
64/64 [==============================] - 3s 43ms/step - loss: 5.4616e-04 - val_loss: 5.6270e-04
Epoch 91/100
64/64 [==============================] - 3s 43ms/step - loss: 4.5601e-04 - val_loss: 5.5043e-04
Epoch 92/100
64/64 [==============================] - 3s 43ms/step - loss: 4.3344e-04 - val_loss: 4.6876e-04
Epoch 93/100
64/64 [==============================] - 3s 42ms/step - loss: 5.3680e-04 - val_loss: 4.5829e-04
Epoch 94/100
64/64 [==============================] - 3s 43ms/step - loss: 7.5234e-04 - val_loss: 6.1782e-04
Epoch 95/100
64/64 [==============================] - 3s 42ms/step - loss: 3.7421e-04 - val_loss: 3.6062e-04
Epoch 96/100
64/64 [==============================] - 3s 43ms/step - loss: 3.9064e-04 - val_loss: 5.2667e-04
Epoch 97/100
64/64 [==============================] - 3s 43ms/step - loss: 4.5003e-04 - val_loss: 4.0708e-04
Epoch 98/100
64/64 [==============================] - 3s 43ms/step - loss: 5.4694e-04 - val_loss: 0.0011
Epoch 99/100
64/64 [==============================] - 3s 42ms/step - loss: 5.4764e-04 - val_loss: 7.6580e-04
Epoch 100/100
64/64 [==============================] - 3s 43ms/step - loss: 5.1314e-04 - val_loss: 4.5973e-04

png

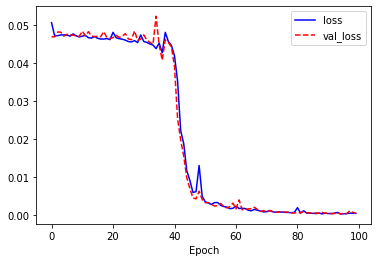
loss와 val_loss는 40에포크를 넘어가면서 매우 가파르게 줄어들어 0에 가까워집니다. val_loss는 변동폭이 loss보다 크지만 전체적으로는 계속 감소하는 경향을 보입니다. 학습이 매우 잘 된 것으로 보입니다.

이번에는 실제로 테스트 데이터에 얼마나 정확하게 값을 예측하는지 확인해봅니다.

model.evaluate(X[2560:], Y[2560:])
prediction=model.predict(X[2560:2560+5])

# 5개 테스트 데이터에 대한 예측을 표시합니다. 
for i in range(5): 
  print(Y[2560+i], '\t', prediction[i][0], '\tdiff:', abs(prediction[i][0] - Y[2560+i]))

prediction = model.predict(X[2560:])
fail = 0
for i in range(len(prediction)):
  # 오차가 0.04 이상이면 오답입니다. 
  if abs(prediction[i][0] - Y[2560+i]) > 0.04:
    fail +=1

print('correctness:', (440-fail)/440*100, '%')

14/14 [==============================] - 0s 13ms/step - loss: 3.9453e-04
0.009316712705671063 	 0.02192213 	diff: 0.012605417432010898
0.1595728709352136 	 0.15154022 	diff: 0.008032651151430648
0.343633615267837 	 0.33932722 	diff: 0.004306399119460513
0.047836290850227836 	 0.03347582 	diff: 0.014360470875090126
0.07471709800989841 	 0.06377047 	diff: 0.01094662500651096
correctness: 95.9090909090909 %

테스트 데이터에 대한 loss는 0에 가까운 값이 나오고, 다섯 개의 샘플에 대한 오차도 0.04를 넘는 값이 없습니다. 또한 정확도 역시, 95.9%로 거의 96%에 가까운 것을 확인할 수 있습니다.

곱셈문제를 푸는데 있어서 LSTM이 보다 적합하다는 것을 알 수 있습니다.

다음 포스트에서는 GRU레이어와 임베딩레이어에 대해 학습하도록 합니다.

IV. 연습 파일

구글 Colab에서 직접 연습해보자

VI. Reference

김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.

Different between CNN，RNN（Quote） Retrieved from https://medium.com/@Aj.Cheng/different-between-cnn-rnn-quote-7c224795db58 ↩︎
1997년 셉 호흐라이터(Sepp Hochreiter) 유르겐 슈미트후버(Jurgen Schmidhuber)에 의해 제안됨, (S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural Computation, 1997. https://www.bioinf.jku.at/publications/older/2604.pdf ↩︎
Olah, Christopher. “Understanding LSTM Networks.” Understanding LSTM Networks – Colah’s Blog, colah.github.io/posts/2015-08-Understanding-LSTMs/ ↩︎