Tensorflow 2.0 Tutorial ch6.3 - Fashion MNIST with CNN 실습

Deep Learning, 딥러닝, 텐서플로 2.0, Python, Tensorflow 2.0, 텐서플로 2.0 튜토리얼, Tensorflow 2.0 Tutorial
Page content

공지

  • 본 Tutorial은 교재 시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다.

  • 강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 반드시 교재를 구매하실 것을 권해드립니다.

  • 본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.

Tutorial

이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.

I. 개요

이번 장은 앞에서 이론만 설명했기 때문에 이번에는 실습 위주로 진행합니다. 컨볼루션 레이어와 풀링 레이어, 드롭아웃을 사용해서 분류 문제를 푸는데 어떻게 해야 성능이 개선 되는지 알아봅니다.

II. 데이터 불러오기 및 정규화

5장에서 배운 내용을 근거로 데이터를 불러오고 정규화를 진행합니다.

import tensorflow as tf
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_X, train_Y), (test_X, test_Y) = fashion_mnist.load_data()

train_X = train_X / 255.0
test_X = test_X / 255.0

Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
32768/29515 [=================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26427392/26421880 [==============================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
8192/5148 [===============================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 0s 0us/step

그런데, 6장에서는 Conv2D레이어로 컨볼루션 연산을 수행해야 합니다. 이미지는 보통 채널을 가지고 있고(컬러 이미지는 RGB의 3채널, 흑백 이미지는 1채널), Conv2D레이어는 채널을 가진 형태의 데이터를 받도록 기본적으로 설정되어 있기 때문에 예제 6.5에서는 채널을 갖도록 데이터의 Shape를 바꿔줍니다.

# reshape 이전
print(train_X.shape, test_X.shape)

train_X = train_X.reshape(-1, 28, 28, 1)
test_X = test_X.reshape(-1, 28, 28, 1)

# reshape 이후
print(train_X.shape, test_X.shape)

(60000, 28, 28) (10000, 28, 28)
(60000, 28, 28, 1) (10000, 28, 28, 1)

Fashion MNIST데이터를 구성하는 흑백 이미지는 1개의 채널을 갖기 때문에 reshape() 함수를 사용해 데이터의 가장 뒤쪽에 채널 차원을 추가합니다. 이 작업으로 데이터 수는 달라지지는 않습니다.

데이터를 확인하는 시각화를 진행합니다.

import matplotlib.pyplot as plt

# 전체 그래프의 크기를 width = 10, height = 10으로 지정합니다. 
plt.figure(figsize=(10, 10))
for c in range(16): 
  # 4행 4열로 지정한 그리드에서 c+1번째의 칸에 그래프를 그립니다. 1~16번째 칸을 채우게 됩니다. 
  plt.subplot(4,4,c+1)
  plt.imshow(train_X[c].reshape(28,28), cmap='gray')

plt.show()

# 훈련 데이터이 1~16번째 까지의 라벨 프린트합니다. 
print(train_Y[:16])

png

[9 0 0 3 0 2 7 2 5 5 0 9 5 5 7 9]

라벨의 정의는 아래와 같습니다.

라벨 범주
0 티셔츠/상의
1 바지
2 스웨터
3 드레스
4 코트
5 샌들
6 셔츠
7 운동화
8 가방
9 부츠

라벨의 정의와 비교해보면, 라벨이 잘 분류되어 있는 것을 확인할 수 있습니다. 이제 모델을 생성합니다.

III. 딥러닝 모델 생성

(1) 컨볼루션 신경망 모델 정의

컨볼루션 신경망 모델 정의는 풀링 레이어 또는 드롭아웃 없이 정의된 모델을 말합니다.

model = tf.keras.Sequential([
  tf.keras.layers.Conv2D(input_shape=(28,28,1), kernel_size=(3,3), filters=16),
  tf.keras.layers.Conv2D(kernel_size=(3,3), filters=32), 
  tf.keras.layers.Conv2D(kernel_size=(3,3), filters=64), 
  tf.keras.layers.Flatten(), 
  tf.keras.layers.Dense(units=128, activation='relu'), 
  tf.keras.layers.Dense(units=10, activation='softmax')                             
])

model.compile(optimizer=tf.keras.optimizers.Adam(), 
              loss='sparse_categorical_crossentropy', 
              metrics=['accuracy'])

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 26, 26, 16)        160       
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 24, 24, 32)        4640      
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 22, 22, 64)        18496     
_________________________________________________________________
flatten (Flatten)            (None, 30976)             0         
_________________________________________________________________
dense (Dense)                (None, 128)               3965056   
_________________________________________________________________
dense_1 (Dense)              (None, 10)                1290      
=================================================================
Total params: 3,989,642
Trainable params: 3,989,642
Non-trainable params: 0
_________________________________________________________________

Conv2D의 인수에 대해 정리하도록 합니다.

  • kernel_size: 필터 행렬의 크기를 말하며, 수용 영역(receptive filed)이라고 불리워집니다. 앞의 숫자는 높이, 뒤의 숫자는 너비이고, 숫자를 하나만 쓸 경우 높이와 너비를 동일한 값으로 사용한다는 뜻입니다.1
  • filters: 필터의 개수를 의미하며, 네트워크가 깊어질수록 2배씩 늘려나갑니다.
!nvidia-smi

Tue Apr 21 06:56:00 2020       
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 440.64.00    Driver Version: 418.67       CUDA Version: 10.1     |
|-------------------------------+----------------------+----------------------+
| GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
|===============================+======================+======================|
|   0  Tesla K80           Off  | 00000000:00:04.0 Off |                    0 |
| N/A   31C    P8    26W / 149W |      0MiB / 11441MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
                                                                               
+-----------------------------------------------------------------------------+
| Processes:                                                       GPU Memory |
|  GPU       PID   Type   Process name                             Usage      |
|=============================================================================|
|  No running processes found                                                 |
+-----------------------------------------------------------------------------+

위 명령어는 현재 구글 코랩에서 지원하는 GPU의 성능입니다. Tesla K80을 사용하고 있습니다.

구글 코랩에서는 무료로 GPU를 사용할 수 있도록 도와줍니다. 하드웨어 가속기를 사용하려면 [메뉴]-[런타임]-[런타임 유형 변경]-[하드웨어 가속기]-[GPU]로 지정하면 됩니다.

(2) 컨볼루션 신경망 모델 학습

신경망 모형을 학습하는데, 시간이 조금 소요되니 참고바란다. (약 10분)

history = model.fit(train_X, train_Y, epochs=25, validation_split=0.25)

Epoch 1/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.4740 - accuracy: 0.8287 - val_loss: 0.3986 - val_accuracy: 0.8565
Epoch 2/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.3461 - accuracy: 0.8746 - val_loss: 0.3651 - val_accuracy: 0.8668
Epoch 3/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.2911 - accuracy: 0.8937 - val_loss: 0.3697 - val_accuracy: 0.8661
Epoch 4/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.2546 - accuracy: 0.9053 - val_loss: 0.3870 - val_accuracy: 0.8669
Epoch 5/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.2226 - accuracy: 0.9174 - val_loss: 0.4187 - val_accuracy: 0.8670
Epoch 6/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1904 - accuracy: 0.9283 - val_loss: 0.4704 - val_accuracy: 0.8665
Epoch 7/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1736 - accuracy: 0.9356 - val_loss: 0.4938 - val_accuracy: 0.8703
Epoch 8/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1495 - accuracy: 0.9454 - val_loss: 0.5293 - val_accuracy: 0.8694
Epoch 9/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1424 - accuracy: 0.9478 - val_loss: 0.5503 - val_accuracy: 0.8654
Epoch 10/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1280 - accuracy: 0.9535 - val_loss: 0.6191 - val_accuracy: 0.8575
Epoch 11/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1203 - accuracy: 0.9556 - val_loss: 0.7030 - val_accuracy: 0.8626
Epoch 12/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1131 - accuracy: 0.9596 - val_loss: 0.7228 - val_accuracy: 0.8656
Epoch 13/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1024 - accuracy: 0.9621 - val_loss: 0.8023 - val_accuracy: 0.8632
Epoch 14/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.1020 - accuracy: 0.9636 - val_loss: 0.7895 - val_accuracy: 0.8690
Epoch 15/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0900 - accuracy: 0.9688 - val_loss: 1.0383 - val_accuracy: 0.8581
Epoch 16/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0933 - accuracy: 0.9669 - val_loss: 0.8304 - val_accuracy: 0.8649
Epoch 17/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0816 - accuracy: 0.9712 - val_loss: 1.0017 - val_accuracy: 0.8661
Epoch 18/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0782 - accuracy: 0.9715 - val_loss: 0.9552 - val_accuracy: 0.8653
Epoch 19/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0745 - accuracy: 0.9748 - val_loss: 1.0168 - val_accuracy: 0.8631
Epoch 20/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0787 - accuracy: 0.9724 - val_loss: 1.0362 - val_accuracy: 0.8627
Epoch 21/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0675 - accuracy: 0.9759 - val_loss: 1.1104 - val_accuracy: 0.8577
Epoch 22/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0725 - accuracy: 0.9764 - val_loss: 1.2423 - val_accuracy: 0.8603
Epoch 23/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0644 - accuracy: 0.9783 - val_loss: 1.2578 - val_accuracy: 0.8589
Epoch 24/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0650 - accuracy: 0.9790 - val_loss: 1.3452 - val_accuracy: 0.8589
Epoch 25/25
1407/1407 [==============================] - 13s 9ms/step - loss: 0.0655 - accuracy: 0.9791 - val_loss: 1.2309 - val_accuracy: 0.8605

이렇게 생성된 모형은 시각화로 다시 확인한다.

import matplotlib.pyplot as plt
plt.figure(figsize=(12, 4))

plt.subplot(1,2,1)
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()

plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], 'g-', label='accuracy')
plt.plot(history.history['val_accuracy'], 'r--', label='val_accuracy')
plt.xlabel('Epoch')
plt.ylim(0.7, 1)
plt.legend()

plt.show()

model.evaluate(test_X, test_Y, verbose=0)

png

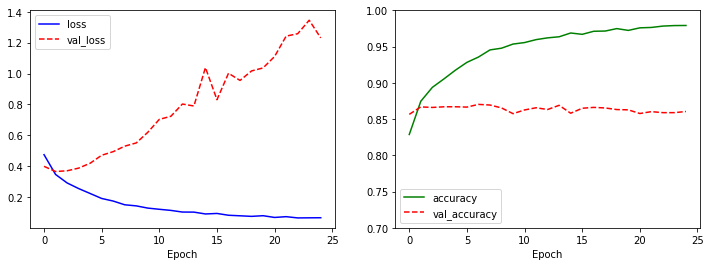
[1.3350350856781006, 0.855400025844574]

왼쪽 그래프를 확인하면, loss는 감소하고, 대신 var_loss는 증가하는 전형적인 과적합의 형태를 나타냅니다. 이럴경우 모형에도 악영향이 있어서, 오히려 단순 딥러닝 모형의 성과가 더 좋은 것을 확인할 수 있습니다.

  • 테스트 데이터의 85.21% Vs. 5.3장의 Dense Layer 88.5%

즉, 컨볼루션 레이어만 사용할 경우, 오히려 성능이 더 좋지 않은 것을 확인할 수 있었습니다. 이제 성능을 개선해봅니다.

(3) 풀링 레이어, 드롭아웃 레이어 추가 (약 10분)

model = tf.keras.Sequential([
  tf.keras.layers.Conv2D(input_shape=(28,28,1), kernel_size=(3,3), filters=32), 
  tf.keras.layers.MaxPool2D(strides=(2,2)), 
  tf.keras.layers.Conv2D(kernel_size=(3,3), filters=64), 
  tf.keras.layers.MaxPool2D(strides=(2,2)), 
  tf.keras.layers.Conv2D(kernel_size=(3,3), filters=128), 
  tf.keras.layers.Flatten(), 
  tf.keras.layers.Dense(units=128, activation='relu'), 
  tf.keras.layers.Dropout(rate=0.3),
  tf.keras.layers.Dense(units=10, activation='softmax')                             
])

model.compile(optimizer=tf.keras.optimizers.Adam(), 
              loss='sparse_categorical_crossentropy', 
              metrics=['accuracy'])

model.summary()

Model: "sequential_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_9 (Conv2D)            (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_10 (Conv2D)           (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_5 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
conv2d_11 (Conv2D)           (None, 3, 3, 128)         73856     
_________________________________________________________________
flatten_3 (Flatten)          (None, 1152)              0         
_________________________________________________________________
dense_6 (Dense)              (None, 128)               147584    
_________________________________________________________________
dropout_2 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_7 (Dense)              (None, 10)                1290      
=================================================================
Total params: 241,546
Trainable params: 241,546
Non-trainable params: 0
_________________________________________________________________

이번에 추가된 인수는 MaxPool2D(strides=(2,2))와 Dropout(rate=0.3)입니다.

  • strides: 필터가 계산 과정에서 한 스텝마다 이동하는 크기입니다. 기본값은 (1,1)이고, (2,2) 등으로 설정할 경우 한 칸씩 건너뛰면서 계산하게 되니다. strides=1일 때와 2일 때의 결과 이미지의 크기에 영향을 줍니다.
  • rate: 제외할 뉴런의 비율을 나타냅니다.

여기서 확인해야 하는 개수 Param의 개수입니다.

기존 3,989,642에서 241,546으로 대폭 줄어든 것을 확인할 수 있습니다. 이는 Flatten에 들어오는 Params의 개수가 기존 (None, 30976)에 비해 (None, 1152)에 비해 크게 줄어들었기 때문입니다.

다시한번, 풀링 레이어와 드롭아웃 레어는 모두 과적합을 줄이는 데 기여합니다.

history = model.fit(train_X, train_Y, epochs=25, validation_split=0.25)

Epoch 1/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.5203 - accuracy: 0.8106 - val_loss: 0.3570 - val_accuracy: 0.8688
Epoch 2/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.3569 - accuracy: 0.8722 - val_loss: 0.3304 - val_accuracy: 0.8747
Epoch 3/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.3195 - accuracy: 0.8839 - val_loss: 0.3127 - val_accuracy: 0.8853
Epoch 4/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2880 - accuracy: 0.8950 - val_loss: 0.2926 - val_accuracy: 0.8943
Epoch 5/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2712 - accuracy: 0.9011 - val_loss: 0.3001 - val_accuracy: 0.8897
Epoch 6/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2548 - accuracy: 0.9080 - val_loss: 0.2878 - val_accuracy: 0.8975
Epoch 7/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2383 - accuracy: 0.9123 - val_loss: 0.3031 - val_accuracy: 0.8920
Epoch 8/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2232 - accuracy: 0.9164 - val_loss: 0.2987 - val_accuracy: 0.9005
Epoch 9/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2132 - accuracy: 0.9200 - val_loss: 0.2983 - val_accuracy: 0.8980
Epoch 10/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.2086 - accuracy: 0.9219 - val_loss: 0.3241 - val_accuracy: 0.8949
Epoch 11/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1937 - accuracy: 0.9284 - val_loss: 0.3066 - val_accuracy: 0.9017
Epoch 12/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1828 - accuracy: 0.9320 - val_loss: 0.3199 - val_accuracy: 0.9020
Epoch 13/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1862 - accuracy: 0.9305 - val_loss: 0.3195 - val_accuracy: 0.9034
Epoch 14/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1720 - accuracy: 0.9360 - val_loss: 0.3504 - val_accuracy: 0.8995
Epoch 15/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1661 - accuracy: 0.9372 - val_loss: 0.3565 - val_accuracy: 0.8953
Epoch 16/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1626 - accuracy: 0.9396 - val_loss: 0.3508 - val_accuracy: 0.9031
Epoch 17/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1567 - accuracy: 0.9406 - val_loss: 0.4112 - val_accuracy: 0.8989
Epoch 18/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1558 - accuracy: 0.9410 - val_loss: 0.3937 - val_accuracy: 0.8933
Epoch 19/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1506 - accuracy: 0.9434 - val_loss: 0.3724 - val_accuracy: 0.9003
Epoch 20/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1444 - accuracy: 0.9461 - val_loss: 0.4128 - val_accuracy: 0.9000
Epoch 21/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1397 - accuracy: 0.9482 - val_loss: 0.4300 - val_accuracy: 0.8975
Epoch 22/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1373 - accuracy: 0.9492 - val_loss: 0.4505 - val_accuracy: 0.9008
Epoch 23/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1377 - accuracy: 0.9497 - val_loss: 0.5026 - val_accuracy: 0.8955
Epoch 24/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1383 - accuracy: 0.9498 - val_loss: 0.5038 - val_accuracy: 0.8881
Epoch 25/25
1407/1407 [==============================] - 10s 7ms/step - loss: 0.1293 - accuracy: 0.9516 - val_loss: 0.5226 - val_accuracy: 0.8945

import matplotlib.pyplot as plt
plt.figure(figsize=(12, 4))

plt.subplot(1,2,1)
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()

plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], 'g-', label='accuracy')
plt.plot(history.history['val_accuracy'], 'r--', label='val_accuracy')
plt.xlabel('Epoch')
plt.ylim(0.7, 1)
plt.legend()

plt.show()

model.evaluate(test_X, test_Y, verbose=0)

png

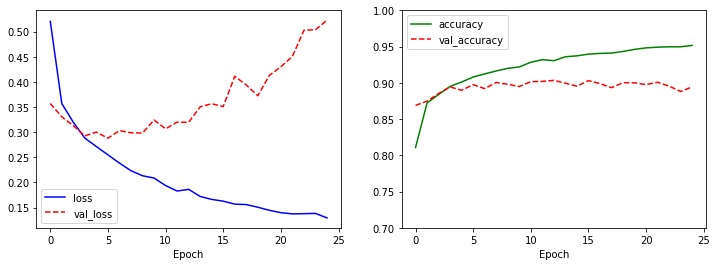
[0.5307855606079102, 0.8906999826431274]

var_loss는 여전히 증가하지만, val_accuracy는 일정한 수준에 머무르고 있습니다. 분류 성적도 89.06%로 약 0.4% 높은 수치가 나옵니다 (종전: 88.77%). 그러나, 확실히 컨볼루션 레이어만 활용했을 때 보다는 확실히 좋은 결과가 나온 것을 확인할 수 있습니다.

이보다 더 좋은 성과를 낼 수 있습니다. Fashion MNIST의 공식 깃허브 저장소에는 테스트 데이터 분류 성적이 95% 이상을 달성한 방법들도 존재합니다. 2

IV. 연습 파일

V. Reference

김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.

  1. 이 부분은 교재 p. 145~147에 이미지로 설명이 잘 되어 있으니 참고하기를 바랍니다. ↩︎

  2. https://github.com/zalandoresearch/fashion-mnist#benchmark 파이썬 실력이 되시는 분들은 95%이상의 성능을 보유한 Repo에 있는 코드를 직접 가져와 응용하는 것도 큰 도움이 될 수 있습니다. ↩︎