Tensorflow 2.0 Tutorial ch5.3 - Fashion MNIST
공지
-
본 Tutorial은 교재
시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다. -
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 반드시 교재를 구매하실 것을 권해드립니다.

- 본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.
Tutorial
이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.
- Google Colab Tensorflow 2.0 Installation
- Tensorflow 2.0 Tutorial ch3.3.1 - 난수 생성 및 시그모이드 함수
- Tensorflow 2.0 Tutorial ch3.3.2 - 난수 생성 및 시그모이드 함수 편향성
- Tensorflow 2.0 Tutorial ch3.3.3 - 첫번째 신경망 네트워크 - AND
- Tensorflow 2.0 Tutorial ch3.3.4 - 두번째 신경망 네트워크 - OR
- Tensorflow 2.0 Tutorial ch3.3.5 - 세번째 신경망 네트워크 - XOR
- Tensorflow 2.0 Tutorial ch4.1 - 선형회귀
- Tensorflow 2.0 Tutorial ch4.2 - 다항회귀
- Tensorflow 2.0 Tutorial ch4.3 - 딥러닝 네트워크를 이용한 회귀
- Tensorflow 2.0 Tutorial ch4.4 - 보스턴 주택 가격 데이터세트
- Tensorflow 2.0 Tutorial ch5.1 - 분류
- Tensorflow 2.0 Tutorial ch5.2 - 다항분류
I. 개요1
MNIST는 머신러닝의 고전적인 문제로 손으로 쓴 숫자 글씨를 모아놓은 데이터 세트이며, Fashion MNIST는 손글씨가 아닌 옷과 신발, 가방의 이미지 등을 모아 놓는다. 그레이스케일 이미지2라는 점과 범주의 수가 10개라는 점, 각 이미지의 크기가 28X28 픽셀이라는 점은 MNIST와 동일하지만 좀 더 어려운 문제로 평가됩니다.
라벨의 정의는 아래와 같습니다.
| 라벨 | 범주 |
|---|---|
| 0 | 티셔츠/상의 |
| 1 | 바지 |
| 2 | 스웨터 |
| 3 | 드레스 |
| 4 | 코트 |
| 5 | 샌들 |
| 6 | 셔츠 |
| 7 | 운동화 |
| 8 | 가방 |
| 9 | 부츠 |
II. 데이터 불러오기
Fashion MNIST 데이터세트는 tf.keras에 기본으로 탑재가 되어 있기 때문에 간단하게 불러올 수 있다.
# 텐서플로 2 버전 선택
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import pandas as pd
import tensorflow as tf
from tabulate import tabulate
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_X, train_Y), (test_X, test_Y) = fashion_mnist.load_data()
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
32768/29515 [=================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26427392/26421880 [==============================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
8192/5148 [===============================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 0s 0us/step
print(len(train_X), len(test_X))
60000 10000
훈련 데이터는 60,000장, 테스트 데이터는 10,000장의 패션 이미지를 포함하고 있습니다. 데이터세트를 불러온 후에는 이 데이터가 어떻게 생겼는지 확인해봐야 합니다.
import matplotlib.pyplot as plt
plt.imshow(train_X[0], cmap='gray')
plt.colorbar()
plt.show()
print(train_Y[0])
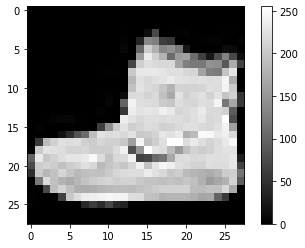
9
imshow() 이미지를 그래프의 형태로 표시 할 수 있고, colorbar() 함수는 그래프 옆에 색상의 값 정보를 (bar) 형태로 표시할 수 있습니다. 데이터의 이미지가 0에서 255까지의 값을 가지는 28X28 픽셀 크기의 2차원 이미지라는 것을 확인할 수 있습니다.
III. 데이터 정규화
데이터를 정규화를 진행합니다. 여기에서는 최대값과 최소값을 이미 알고 있기 때문에 이미지의 각 픽셀값을 255로 나누기만 하면 0.0~1.0사이의 값으로 정규화됩니다.
train_X = train_X / 255.0
test_X = test_X / 255.0
print(train_X[0])
[[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0.00392157 0. 0. 0.05098039 0.28627451 0.
0. 0.00392157 0.01568627 0. 0. 0.
0. 0.00392157 0.00392157 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0.01176471 0. 0.14117647 0.53333333 0.49803922 0.24313725
0.21176471 0. 0. 0. 0.00392157 0.01176471
0.01568627 0. 0. 0.01176471]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0.02352941 0. 0.4 0.8 0.69019608 0.5254902
0.56470588 0.48235294 0.09019608 0. 0. 0.
0. 0.04705882 0.03921569 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0.60784314 0.9254902 0.81176471 0.69803922
0.41960784 0.61176471 0.63137255 0.42745098 0.25098039 0.09019608
0.30196078 0.50980392 0.28235294 0.05882353]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.00392157
0. 0.27058824 0.81176471 0.8745098 0.85490196 0.84705882
0.84705882 0.63921569 0.49803922 0.4745098 0.47843137 0.57254902
0.55294118 0.34509804 0.6745098 0.25882353]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0.00392157 0.00392157 0.00392157
0. 0.78431373 0.90980392 0.90980392 0.91372549 0.89803922
0.8745098 0.8745098 0.84313725 0.83529412 0.64313725 0.49803922
0.48235294 0.76862745 0.89803922 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.71764706 0.88235294 0.84705882 0.8745098 0.89411765
0.92156863 0.89019608 0.87843137 0.87058824 0.87843137 0.86666667
0.8745098 0.96078431 0.67843137 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0.75686275 0.89411765 0.85490196 0.83529412 0.77647059
0.70588235 0.83137255 0.82352941 0.82745098 0.83529412 0.8745098
0.8627451 0.95294118 0.79215686 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0.00392157 0.01176471 0.
0.04705882 0.85882353 0.8627451 0.83137255 0.85490196 0.75294118
0.6627451 0.89019608 0.81568627 0.85490196 0.87843137 0.83137255
0.88627451 0.77254902 0.81960784 0.20392157]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0.02352941 0.
0.38823529 0.95686275 0.87058824 0.8627451 0.85490196 0.79607843
0.77647059 0.86666667 0.84313725 0.83529412 0.87058824 0.8627451
0.96078431 0.46666667 0.65490196 0.21960784]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0.01568627 0. 0.
0.21568627 0.9254902 0.89411765 0.90196078 0.89411765 0.94117647
0.90980392 0.83529412 0.85490196 0.8745098 0.91764706 0.85098039
0.85098039 0.81960784 0.36078431 0. ]
[0. 0. 0.00392157 0.01568627 0.02352941 0.02745098
0.00784314 0. 0. 0. 0. 0.
0.92941176 0.88627451 0.85098039 0.8745098 0.87058824 0.85882353
0.87058824 0.86666667 0.84705882 0.8745098 0.89803922 0.84313725
0.85490196 1. 0.30196078 0. ]
[0. 0.01176471 0. 0. 0. 0.
0. 0. 0. 0.24313725 0.56862745 0.8
0.89411765 0.81176471 0.83529412 0.86666667 0.85490196 0.81568627
0.82745098 0.85490196 0.87843137 0.8745098 0.85882353 0.84313725
0.87843137 0.95686275 0.62352941 0. ]
[0. 0. 0. 0. 0.07058824 0.17254902
0.32156863 0.41960784 0.74117647 0.89411765 0.8627451 0.87058824
0.85098039 0.88627451 0.78431373 0.80392157 0.82745098 0.90196078
0.87843137 0.91764706 0.69019608 0.7372549 0.98039216 0.97254902
0.91372549 0.93333333 0.84313725 0. ]
[0. 0.22352941 0.73333333 0.81568627 0.87843137 0.86666667
0.87843137 0.81568627 0.8 0.83921569 0.81568627 0.81960784
0.78431373 0.62352941 0.96078431 0.75686275 0.80784314 0.8745098
1. 1. 0.86666667 0.91764706 0.86666667 0.82745098
0.8627451 0.90980392 0.96470588 0. ]
[0.01176471 0.79215686 0.89411765 0.87843137 0.86666667 0.82745098
0.82745098 0.83921569 0.80392157 0.80392157 0.80392157 0.8627451
0.94117647 0.31372549 0.58823529 1. 0.89803922 0.86666667
0.7372549 0.60392157 0.74901961 0.82352941 0.8 0.81960784
0.87058824 0.89411765 0.88235294 0. ]
[0.38431373 0.91372549 0.77647059 0.82352941 0.87058824 0.89803922
0.89803922 0.91764706 0.97647059 0.8627451 0.76078431 0.84313725
0.85098039 0.94509804 0.25490196 0.28627451 0.41568627 0.45882353
0.65882353 0.85882353 0.86666667 0.84313725 0.85098039 0.8745098
0.8745098 0.87843137 0.89803922 0.11372549]
[0.29411765 0.8 0.83137255 0.8 0.75686275 0.80392157
0.82745098 0.88235294 0.84705882 0.7254902 0.77254902 0.80784314
0.77647059 0.83529412 0.94117647 0.76470588 0.89019608 0.96078431
0.9372549 0.8745098 0.85490196 0.83137255 0.81960784 0.87058824
0.8627451 0.86666667 0.90196078 0.2627451 ]
[0.18823529 0.79607843 0.71764706 0.76078431 0.83529412 0.77254902
0.7254902 0.74509804 0.76078431 0.75294118 0.79215686 0.83921569
0.85882353 0.86666667 0.8627451 0.9254902 0.88235294 0.84705882
0.78039216 0.80784314 0.72941176 0.70980392 0.69411765 0.6745098
0.70980392 0.80392157 0.80784314 0.45098039]
[0. 0.47843137 0.85882353 0.75686275 0.70196078 0.67058824
0.71764706 0.76862745 0.8 0.82352941 0.83529412 0.81176471
0.82745098 0.82352941 0.78431373 0.76862745 0.76078431 0.74901961
0.76470588 0.74901961 0.77647059 0.75294118 0.69019608 0.61176471
0.65490196 0.69411765 0.82352941 0.36078431]
[0. 0. 0.29019608 0.74117647 0.83137255 0.74901961
0.68627451 0.6745098 0.68627451 0.70980392 0.7254902 0.7372549
0.74117647 0.7372549 0.75686275 0.77647059 0.8 0.81960784
0.82352941 0.82352941 0.82745098 0.7372549 0.7372549 0.76078431
0.75294118 0.84705882 0.66666667 0. ]
[0.00784314 0. 0. 0. 0.25882353 0.78431373
0.87058824 0.92941176 0.9372549 0.94901961 0.96470588 0.95294118
0.95686275 0.86666667 0.8627451 0.75686275 0.74901961 0.70196078
0.71372549 0.71372549 0.70980392 0.69019608 0.65098039 0.65882353
0.38823529 0.22745098 0. 0. ]
[0. 0. 0. 0. 0. 0.
0. 0.15686275 0.23921569 0.17254902 0.28235294 0.16078431
0.1372549 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.
0. 0. 0. 0. ]]
모든 데이터가 0에서 1사이의 값을 갖기 때문에 데이터 정규화가 잘 된 것을 알 수 있습니다. 이 다음에 진행해야 하는 것은 train_Y와 test_Y에 원-핫 인코딩으로 바꾸는 부분입니다. (이전 강의 참조)
to_categorical 함수를 이용해 정답 행렬을 원-핫 인코딩으로 바꾸면 아래와 같습니다.
train_Y = tf.keras.utils.to_categorical(train_Y, num_classes=10)
test_Y = tf.keras.utils.to_categorical(test_Y, num_classes=10)
이 때 9는 [0,0,0,0,0,0,0,0,0,1]로 바뀔 것입니다. 만약에 분류해야 하는 것이 100이라면 어떻게 해야 할까요? 이러한 비효율성을 제거해줄 때 희소 행렬이라는 원리를 이용합니다. 행렬이 클 경우 수 많은 0을 위한 메모리를 모두 확보하는 것 자체가 매우 시스템적으로 낭비이기 때문입니다. 이렇게 이미지 분류의 경우에는 원-핫 인코딩보다는 희소행렬 원리를 이용해서 작성하는 경우가 많으니 참고하기를 바랍니다.
IV. 딥러닝 모형
이제 모형을 생성합니다.
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28,28)),
tf.keras.layers.Dense(units=128, activation="relu"),
tf.keras.layers.Dense(units=10, activation="softmax")
])
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten (Flatten) (None, 784) 0
_________________________________________________________________
dense (Dense) (None, 128) 100480
_________________________________________________________________
dense_1 (Dense) (None, 10) 1290
=================================================================
Total params: 101,770
Trainable params: 101,770
Non-trainable params: 0
_________________________________________________________________
- 여기에서 주의해서 봐야하는 것은
loss에sparse_categorical_crossentropy로 기재하면 별도의 데이터 전처리 없이 희소 행렬을 나타내는 데이터를 정답 행렬로 사용할 수 있습니다. - 또한,
Dense대신에Flatten이 사용되었는데, 이는 다차원 데이터를 1차원으로 정렬하는 역할을 합니다. Adam()의 기본값은 0,001로 매우 작습니다.3
history = model.fit(train_X, train_Y, epochs=25, validation_split=0.25)
Epoch 1/25
1407/1407 [==============================] - 4s 3ms/step - loss: 0.5262 - accuracy: 0.8160 - val_loss: 0.4230 - val_accuracy: 0.8477
Epoch 2/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.3936 - accuracy: 0.8608 - val_loss: 0.3669 - val_accuracy: 0.8703
Epoch 3/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.3509 - accuracy: 0.8733 - val_loss: 0.3639 - val_accuracy: 0.8670
Epoch 4/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.3262 - accuracy: 0.8818 - val_loss: 0.3671 - val_accuracy: 0.8691
Epoch 5/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.3081 - accuracy: 0.8868 - val_loss: 0.3514 - val_accuracy: 0.8727
Epoch 6/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2907 - accuracy: 0.8921 - val_loss: 0.3476 - val_accuracy: 0.8807
Epoch 7/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2789 - accuracy: 0.8980 - val_loss: 0.3285 - val_accuracy: 0.8827
Epoch 8/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2637 - accuracy: 0.9017 - val_loss: 0.3161 - val_accuracy: 0.8869
Epoch 9/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2552 - accuracy: 0.9060 - val_loss: 0.3268 - val_accuracy: 0.8851
Epoch 10/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2474 - accuracy: 0.9093 - val_loss: 0.3391 - val_accuracy: 0.8808
Epoch 11/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2375 - accuracy: 0.9106 - val_loss: 0.3299 - val_accuracy: 0.8833
Epoch 12/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2310 - accuracy: 0.9146 - val_loss: 0.3291 - val_accuracy: 0.8833
Epoch 13/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2203 - accuracy: 0.9174 - val_loss: 0.3204 - val_accuracy: 0.8880
Epoch 14/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2149 - accuracy: 0.9196 - val_loss: 0.3294 - val_accuracy: 0.8883
Epoch 15/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2075 - accuracy: 0.9214 - val_loss: 0.3354 - val_accuracy: 0.8821
Epoch 16/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.2025 - accuracy: 0.9251 - val_loss: 0.3220 - val_accuracy: 0.8922
Epoch 17/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1949 - accuracy: 0.9264 - val_loss: 0.3148 - val_accuracy: 0.8927
Epoch 18/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1918 - accuracy: 0.9291 - val_loss: 0.3359 - val_accuracy: 0.8899
Epoch 19/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1844 - accuracy: 0.9319 - val_loss: 0.3367 - val_accuracy: 0.8891
Epoch 20/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1809 - accuracy: 0.9321 - val_loss: 0.3369 - val_accuracy: 0.8893
Epoch 21/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1766 - accuracy: 0.9352 - val_loss: 0.3314 - val_accuracy: 0.8933
Epoch 22/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1712 - accuracy: 0.9353 - val_loss: 0.3511 - val_accuracy: 0.8892
Epoch 23/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1672 - accuracy: 0.9371 - val_loss: 0.3677 - val_accuracy: 0.8866
Epoch 24/25
1407/1407 [==============================] - 4s 3ms/step - loss: 0.1621 - accuracy: 0.9388 - val_loss: 0.3814 - val_accuracy: 0.8858
Epoch 25/25
1407/1407 [==============================] - 3s 2ms/step - loss: 0.1574 - accuracy: 0.9413 - val_loss: 0.3483 - val_accuracy: 0.8935
V. 모형 결과 확인
학습 출력 결과를 보면 훈련 데이터의 정확도는 점점 증가하고, 검증 데이터의 정확도는 일정한 수준으로 유지됩니다. 전체 학습 과정을 조망하기 위해 history 변수에 저장된 학습 결과를 시각화 합니다.
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 4))
plt.subplot(1,2,1)
plt.plot(history.history['loss'], 'b-', label='loss')
plt.plot(history.history['val_loss'], 'r--', label='val_loss')
plt.xlabel('Epoch')
plt.legend()
plt.subplot(1,2,2)
plt.plot(history.history['accuracy'], 'g-', label='accuracy')
plt.plot(history.history['val_accuracy'], 'r--', label='val_accuracy')
plt.xlabel('Epoch')
plt.ylim(0.7, 1)
plt.legend()
plt.show()
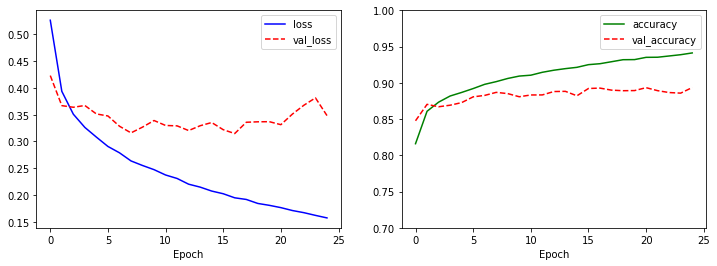
검증 데이터의 손실이 감소하다가 시간이 지날수록 서서히 증가하는 과적합 현상을 확인할 수 있는데, 이를 막기 위해서는 tf.keras.callbacks.EarlyStopping을 사용합니다.
model.evaluate(test_X, test_Y)
313/313 [==============================] - 0s 1ms/step - loss: 0.3830 - accuracy: 0.8877
[0.3830251693725586, 0.8877000212669373]
테스트 데이터에 대한 평가 정확도는 88.5%가 나왔습니다. 괜찮은 수치 같지만, 네트워크 구조 변경과 다른 학습 기법을 사용해서 정확도를 90%이상으로 끌어 올려야 합니다. 이를 컨볼루션 신경망(CNN)에서 그 방법을 확인합니다.
VI. 연습 파일
VII. Reference
김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.
