Tensorflow 2.0 Tutorial ch4.2 - 다항 회귀

2020-04-15

Deep Learning, 딥러닝, 텐서플로 2.0, Python, Tensorflow 2.0, 텐서플로 2.0 튜토리얼, Tensorflow 2.0 Tutorial

Page content

공지

본 Tutorial은 교재 시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다.
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 반드시 교재를 구매하실 것을 권해드립니다.

본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.

Tutorial

이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.

I. 기본개념

비선형 회귀(Nonlinear Regression)는 선형 회귀로는 표현할 수 없는 데이터의 경향성을 설명하기 위한 회귀입니다. 이 가운데 $x^2$, $x^3$ 등의 다항식을 이용한 회귀를 다항회귀(Polynomial Regression)라고 합니다.

즉, 회귀선이 직선 대신 2차 함수, 3차 함수 등의 곡선이 됩니다.

2차 함수 이상의 그래프를 그려도 데이터의 경향성이 잘 나타나는지 확인합니다. 텐서플로를 이용해서 소스코드를 작업합니다.

II. 2차함수 소스코드 및 손실량

import tensorflow as tf
import numpy as np

# 모듈을 가져옵니다. 
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import random
X = [0.3, -0.78, 1.26, 0.03, 1.11, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
Y = [12.27, 14.44, 11.87, 18.75, 17.52, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

# a와 b, c를 랜덤한 값으로 초기화합니다.
a = tf.Variable(random.random())
b = tf.Variable(random.random())
c = tf.Variable(random.random())

# 잔차의 제곱의 평균을 반환하는 함수입니다. 
def compute_loss(): 
  # 책의 본문(p, 83)은 아래처럼 되어 있지만, 에러가 날 것이다. 
  # y_pred = a*X**2 + b*X + c
  y_pred = a * X * X + b * X + c 
  loss = tf.reduce_mean((Y - y_pred) ** 2)
  return loss

optimizer = tf.keras.optimizers.Adam(lr=0.07)

for i in range(1000): 
  # 잔차의 제곱의 평균을 최소화합니다. 
  optimizer.minimize(compute_loss, var_list=[a, b, c])

  if i % 100 == 99: 
    print(i, 'a:', a.numpy(), 'b:', b.numpy(), 'c:', c.numpy(), 'loss:', compute_loss().numpy())

line_x = np.arange(min(X), max(X), 0.01)
line_y = a * line_x * line_x + b * line_x + c

# 그래프를 그립니다.
plt.plot(line_x,line_y,'r-')
plt.plot(X,Y,'bo')
plt.xlabel('Population Growth Rate (%)')
plt.ylabel('Elderly Population Rate (%)')
plt.show()

99 a: 3.840222 b: -5.386301 c: 6.4142933 loss: 69.31381
199 a: 2.823892 b: -4.6838207 c: 10.26055 loss: 31.852983
299 a: 1.3373799 b: -2.4428246 c: 12.872813 loss: 16.335335
399 a: 0.36516348 b: -0.95042753 c: 14.520345 loss: 11.102524
499 a: -0.16323428 b: -0.13958982 c: 15.417201 loss: 9.763081
599 a: -0.41179818 b: 0.24179395 c: 15.83927 loss: 9.500618
699 a: -0.5134157 b: 0.39770818 c: 16.01183 loss: 9.461109
799 a: -0.5495791 b: 0.4531944 c: 16.07324 loss: 9.456543
899 a: -0.56077087 b: 0.47036672 c: 16.092247 loss: 9.45614
999 a: -0.5637749 b: 0.47497624 c: 16.097347 loss: 9.456112

png

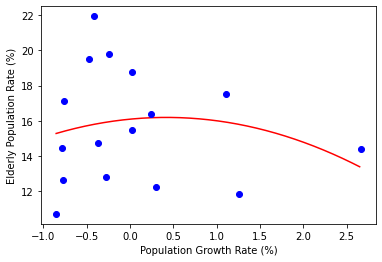
달라진 소스코드는 a와 b를 각각 2차항과 1차항의 계수로 바꿨다는 것입니다. X를 추가하였는데, 기존 a * X + b 코드를 새로운 코드 a * X * X + b * X + c 로 바꾼 것이 중요합니다. 그러나 결과는 직선 회귀선보다 손실이 소량 감소한 것을 확인 할 수 있습니다.

Tensorflow 2.0 Tutorial ch4.1 - 선형회귀와 비교해서 확인해봅니다.

III. 3차함수 소스코드 및 손실량

그렇다면, 3차함수($ax^3+bx^2+cx+d$)의 경우는 어떨까요? 기존코드를 최대한 활용해서 손실량을 확인해봅니다.

import tensorflow as tf
import numpy as np

# 모듈을 가져옵니다. 
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import random
X = [0.3, -0.78, 1.26, 0.03, 1.11, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
Y = [12.27, 14.44, 11.87, 18.75, 17.52, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

# a와 b, c를 랜덤한 값으로 초기화합니다.
a = tf.Variable(random.random())
b = tf.Variable(random.random())
c = tf.Variable(random.random())
d = tf.Variable(random.random())

# 잔차의 제곱의 평균을 반환하는 함수입니다. 
def compute_loss(): 
  # 책의 본문(p, 83)은 아래처럼 되어 있지만, 에러가 날 것이다. 
  # y_pred = a*X**2 + b*X + c
  y_pred = a * X * X * X + b * X * X + c * X + d
  loss = tf.reduce_mean((Y - y_pred) ** 2)
  return loss

optimizer = tf.keras.optimizers.Adam(lr=0.07)

for i in range(1000): 
  # 잔차의 제곱의 평균을 최소화합니다. 
  optimizer.minimize(compute_loss, var_list=[a, b, c])

  if i % 100 == 99: 
    print(i, 'a:', a.numpy(), 'b:', b.numpy(), 'c:', c.numpy(), 'd:', d.numpy(),'loss:', compute_loss().numpy())

line_x = np.arange(min(X), max(X), 0.01)
line_y = a * line_x * line_x * line_x + b * line_x * line_x + c * line_x + d

# 그래프를 그립니다.
plt.plot(line_x,line_y,'r-')
plt.plot(X,Y,'bo')
plt.xlabel('Population Growth Rate (%)')
plt.ylabel('Elderly Population Rate (%)')
plt.show()

99 a: -1.0329757 b: 6.6740055 c: -4.583161 d: 0.52839094 loss: 160.23645
199 a: -2.6273808 b: 11.315129 c: -5.680506 d: 0.52839094 loss: 138.63791
299 a: -3.9567773 b: 14.502094 c: -4.9157133 d: 0.52839094 loss: 130.275
399 a: -4.8310013 b: 16.512175 c: -4.2031274 d: 0.52839094 loss: 127.39865
499 a: -5.3181896 b: 17.629168 c: -3.7981315 d: 0.52839094 loss: 126.6281
599 a: -5.554209 b: 18.170454 c: -3.6022978 d: 0.52839094 loss: 126.46801
699 a: -5.6541195 b: 18.399607 c: -3.5194376 d: 0.52839094 loss: 126.4422
799 a: -5.6911244 b: 18.484484 c: -3.4887505 d: 0.52839094 loss: 126.43897
899 a: -5.703112 b: 18.511978 c: -3.478811 d: 0.52839094 loss: 126.43866
999 a: -5.7064986 b: 18.519741 c: -3.4760025 d: 0.52839094 loss: 126.43864

png

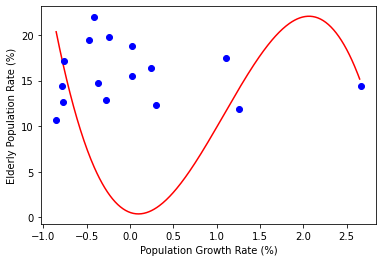
3차 함수가 그려졌지만, 데이터의 경향성을 잘 설명한다보 보기 어렵고, 손실도 매우 커졌음을 확인할 수 있습니다.

1차 함수부터 3차 함수까지 소스코드를 작업한 가장 큰 이유는 어느 것이 가장 적절한 회귀식인지 즉시 알기는 어렵기 때문에 식을 계속 바꿔가며 최적의 회귀식을 찾기 위해 노력해야 한다는 점입니다.

딥러닝을 활용한 회귀는 어떻게 될까요? 또한 무엇을 고려해야 할까요?

다음장에서 조금 더 구체적으로 배우도록 합니다.

VI. 연습 파일

구글 Colab에서 직접 연습해보자

V. Reference

김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.