Tensorflow 2.0 Tutorial ch4.1 - 선형회귀

2020-04-14

Deep Learning, 딥러닝, 텐서플로 2.0, Python, Tensorflow 2.0, 텐서플로 2.0 튜토리얼, Tensorflow 2.0 Tutorial

Page content

공지

본 Tutorial은 교재 시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다.
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 반드시 교재를 구매하실 것을 권해드립니다.

본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.

Tutorial

이전 강의가 궁금하신 분들은 아래에서 선택하여 추가 학습 하시기를 바랍니다.

I. 기본개념

선형 회귀(Linear Regression)는 데이터의 경향성을 가장 잘 설명하는 하나의 직선을 예측하는 것입니다. 선형 회귀에서 주로 사용되는 2차원에서의 직선이란 기울기와 y절편을 가지는 좌표평면 위 점들의 집합니다.

선형 회귀를 이용하면 수치형 데이터의 경향성을 예측할 수 있습니다.

2018년 우리나라의 지역별 인구증가율과 고령인구비율 데이터를 가지고 인구증가율과 고령인구비율 사이에 어떤 경향성이 있는지 선형 회귀로 예측해봅니다.¹

import matplotlib.pyplot as plt
population_inc = [0.3, -0.78, 1.26, 0.03, 1.11, 15.17, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
population_old = [12.27, 14.44, 11.87, 18.75, 17.52, 9.29, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

plt.plot(population_inc, population_old, 'bo')
plt.xlabel('Population Growth Rate')
plt.ylabel('Elderly Population Rate')
plt.show()

png

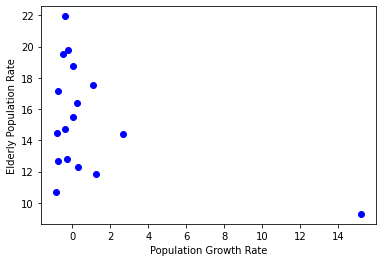
오른쪽 아래에 치우친 하나의 점이 눈에 띄는데, 이것은 극단치(outlier)라고 부르며 일반적인 경향에서 벗어난 사례입니다. 이 극단치는 세종시 데이터인데, 행정수도 이전으로 공무원 등 젊은 인구가 많이 이주해오면서 인구증가율은 높고, 고령인구비율은 낮은 데이터가 만들어진 것 같습니다.

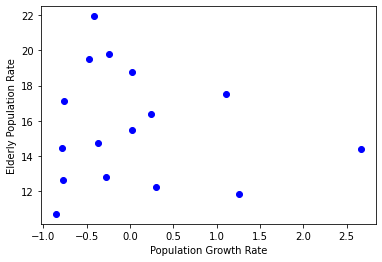
이러한 극단치는 제거하는 것이 일반적인 경향을 파악하기 위해서는 좋습니다.

극단치를 제거하는 코드는 아래와 같습니다.

import matplotlib.pyplot as plt
population_inc = [0.3, -0.78, 1.26, 0.03, 1.11, 15.17, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
population_old = [12.27, 14.44, 11.87, 18.75, 17.52, 9.29, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

population_inc = population_inc[:5] + population_inc[6:]
population_old = population_old[:5] + population_old[6:]

plt.plot(population_inc, population_old, 'bo')
plt.xlabel('Population Growth Rate')
plt.ylabel('Elderly Population Rate')
plt.show()

png

II. 회귀 공식 이해

이제 선형 회귀선을 그려봅니다. 데이터의 경향성을 가장 잘 설명하는 하나의 직선과 각 데이터의 차이를 잔차(residual)라고 합니다. 이런 잔차의 제곱을 최소화하는 알고리즘을 최소제곱법(Least Square Method)라고 부릅니다.

최소제곱법으로 직선 y = ax + b의 a(기울기)와 b(y절편)을 구할 수 있습니다. 중간의 유도과정을 생략하면 공식은 아래와 a, b는 아래와 같습니다.

$$ a = \frac{\sum_{i=1}^{n}\left (y_{i} - \bar{y} \right )\times\left (1 \right )}{\sum_{i=1}^{n}\left (x_{i} - \bar{x}\right )^{2}} $$

$$ b = \bar{y} - a\bar{x} $$

여기서, $x_{i}$, $y_{i}$는 각 데이터 값이고, $\bar{x}$, $\bar{y}$는 데이터의 평균을 의미합니다. 다음 코드는 최소제곱법으로 a와 b를 직접 계산해서 회귀선을 구합니다.

(1) 코드 실습

이제 코드 실습을 진행해봅니다.

import numpy as np
import matplotlib.pyplot as plt

X = [0.3, -0.78, 1.26, 0.03, 1.11, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
Y = [12.27, 14.44, 11.87, 18.75, 17.52, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

# X, Y의 평균을 구합니다. 
x_bar = sum(X) / len(X)
y_bar = sum(Y) / len(Y)

# 최소제곱법으로 a, b를 구합니다. 
a = sum([(y - y_bar) * (x - x_bar) for y, x in list(zip(Y, X))])
a /= sum([(x - x_bar) ** 2 for x in X])
b = y_bar - a * x_bar

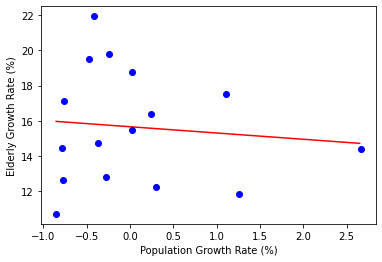
print('a:', a , 'b:', b)

a: -0.355834147915461 b: 15.669317743971302

# 그래프를 그리기 위해 회귀선의 x, y 데이터를 구합니다. 
line_x = np.arange(min(X), max(X), 0.01)
line_y = a * line_x + b

# 붉은색 실선으로 회귀선을 그립니다.
plt.plot(line_x, line_y, 'r-')

plt.plot(X, Y, 'bo')
plt.xlabel('Population Growth Rate (%)')
plt.ylabel('Elderly Growth Rate (%)')

plt.show()

png

(2) 코드 설명

# X, Y의 평균을 구합니다. 
x_bar = sum(X) / len(X)
y_bar = sum(Y) / len(Y)

# 최소제곱법으로 a, b를 구합니다. 
a = sum([(y - y_bar) * (x - x_bar) for y, x in list(zip(Y, X))])
a /= sum([(x - x_bar) ** 2 for x in X])
b = y_bar - a * x_bar

리스트의 총합을 sum()으로 구하고 리스트의 원소 개수를 len()으로 구한 다음 평균을 구합니다.
최소제곱법으로 a, b를 구하는 부분에서 두 개 이상의 리스트를 하나로 묶는 list(zip(list_1, list_2) 기법을 사용했습니다.
참고로 /=는 복합 대입 연산자로써, a = a / sum([(x - x_bar) ** 2 for x in X]) 을 의미합니다.

추가적으로, zip에 대한 추가적인 이해를 돕기 위해 아래 소스코드를 실행하기를 바랍니다.

numbers = [1, 2, 3]
letters = ['a', 'b', 'c']
zipped = zip(numbers, letters)
zipped

<zip at 0x7f5d38875048>

list(zipped)

[(1, 'a'), (2, 'b'), (3, 'c')]

그래프를 그리기 위한 회귀선 x, y 데이터는 아래와 같습니다.

# 그래프를 그리기 위해 회귀선의 x, y 데이터를 구합니다. 
line_x = np.arange(min(X), max(X), 0.01)
line_y = a * line_x + b

이렇게 구한 회귀선에서 데이터의 경향을 알 수 있습니다. X값이 증가할수록 Y값은 감소합니다. 이러한 관계를 음의 상관관계에 있다고 합니다.

III. 텐서플로를 활용한 회귀선 구하기

수식을 적용하지 않고 텐서플로를 구해봅니다.

# 4.4 텐서플로를 이용해서 회귀선 구하기
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import random
X = [0.3, -0.78, 1.26, 0.03, 1.11, 0.24, -0.24, -0.47, -0.77, -0.37, -0.85, -0.41, -0.27, 0.02, -0.76, 2.66]
Y = [12.27, 14.44, 11.87, 18.75, 17.52, 16.37, 19.78, 19.51, 12.65, 14.74, 10.72, 21.94, 12.83, 15.51, 17.14, 14.42]

# a와 b를 랜덤한 값으로 초기화합니다.
a = tf.Variable(random.random())
b = tf.Variable(random.random())

# 잔차의 제곱의 평균을 반환하는 함수입니다. 

def compute_loss(): 
  y_pred = a * X + b
  loss = tf.reduce_mean((Y - y_pred) ** 2)
  return loss

optimizer = tf.optimizers.Adam(lr=0.07)

for i in range(1000): 
  # 잔차의 제곱의 평균을 최소화(minimize) 합니다. 
  optimizer.minimize(compute_loss, var_list=[a,b])

  if i % 100 == 99:
    print(i, 'a:', a.numpy(), 'b:', b.numpy(), 'loss:', compute_loss().numpy())

line_x = np.arange(min(X), max(X), 0.01)
line_y = a * line_x + b

# 그래프를 그립니다. 
plt.plot(line_x, line_y, 'r-')
plt.plot(X, Y, 'bo')
plt.xlabel('Population Growth Rate (%)')
plt.ylabel('Elderly Growth Rate (%)')
plt.show()

99 a: 0.122943394 b: 6.6775966 loss: 90.444305
199 a: -0.115708604 b: 11.171787 loss: 29.961662
299 a: -0.25565353 b: 13.792711 loss: 13.294286
399 a: -0.32145542 b: 15.025314 loss: 10.194582
499 a: -0.34617883 b: 15.488448 loss: 9.813442
599 a: -0.35362422 b: 15.627921 loss: 9.782514
699 a: -0.35542518 b: 15.661658 loss: 9.780862
799 a: -0.35577333 b: 15.668183 loss: 9.780805
899 a: -0.35582697 b: 15.669186 loss: 9.780804
999 a: -0.35583326 b: 15.669302 loss: 9.780804

png

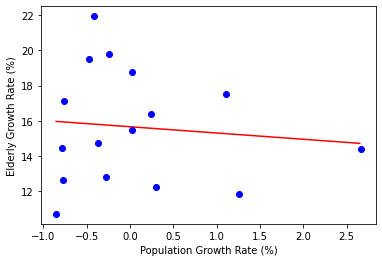
기대출력인 Y에서 실제출력인 y_pred를 빼는데, 이를 잔차라고 부릅니다. 이 잔차의 제곱을 모두 더해서 평균을 낸 값을 loss로 반환합니다.²

optimizer = tf.optimizers.Adam(lr=0.07)

optimizer (최적화 함수)는 미분 계산 및, 가중치 업데이트를 자동으로 진행해주는 편리한 도구입니다.

이 부분에 대한 설명은 교재를 참조하시기를 바랍니다. Adam Optimizer의 학습률은 보통 0.1 ~ 0.0001 사이의 값을 사용합니다.

학습률을 정하는 방법은 하이퍼파라미터 기법으로 많이 사용되는데, 머신러닝 강의를 기억하시는 분은 Grid Search Vs. Random Search에 차이점에 대해 대략적으로 배웠을 겁니다. 그 부분을 기억하시기를 바랍니다.

for i in range(1000): 
  # 잔차의 제곱의 평균을 최소화(minimize) 합니다. 
  optimizer.minimize(compute_loss, var_list=[a,b])

1000번의 학습을 거쳐 a와 b는 잔차의 제곱의 평균을 최소화하는 적절한 값에 도달합니다.

VI. 연습 파일

구글 Colab에서 직접 연습해보자

V. Reference

김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.

통계청, e-지방지표 중 인구 부분 (http://kosis.kr/visual/eRegionJipyo/themaJipyo/eRegionJipyoThemaJipyoView.do) ↩︎
왜 제곱할까요? 잔차를 이해한다면 어려운 것은 아닙니다만 잔차의 경우 음수와 양수 모두가 나올 수 있는데, 이를 모두 더하면 0이 됩니다. 따라서, 절대값을 취하거나 제곱해서 더한후 제곱근을 취하는 방법을 사용합니다. ↩︎