Tensorflow 2.0 Tutorial ch3.3.1 - 난수 생성 및 시그모이드 함수

공지

• 본 Tutorial은 교재 시작하세요 텐서플로 2.0 프로그래밍의 강사에게 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다.
• 강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 반드시 교재를 구매하실 것을 권해드립니다.

• 본 교재 외에 강사가 추가한 내용에 대한 Reference를 확인하셔서, 추가적으로 학습하시는 것을 권유드립니다.

I. 퍼셉트론의 한계 극복

AI는 과거부터 존재하였지만, 여러가지 한계로 인해 연구의 흥망성쇠가 계속적으로 있어왔다. 퍼셉트론의 한계를 지적하는 데 사용됐던, AND, OR, XOR 연산을 할 수 있는 신경망 네트워크를 직접 만들어보자.

II. 난수(Random Number) 생성

신경망을 쉽게 정의하면, 많은 숫자로 구성된 행렬의 의미를 가진다. 행렬을 구성하는 숫자는 처음에 Random으로 지정해주어야 하기 때문에 이러한 작업을 초기화(Initialization)이라 한다. 대중적으로 많이 쓰이는 방법은 Xavier 초기화(Xavier Initialization), He 초기화(He Initialization)가 있다. 이제 난수를 생성해보자.

import tensorflow as tf
print(tf.__version__)

2.2.0-rc2

rand = tf.random.uniform([1], 0, 1)
print(rand)

tf.Tensor([0.10252678], shape=(1,), dtype=float32)

tf.random.uniform 함수는 일종의 균일 분포(uniform distribution)의 난수를 얻을 수 있다. 균일분포의 뜻이란, 정해진 최소값과 최대값 사이의 모든 수가 나올 확률이 동일한 분포에서 수를 뽑는다는 뜻을 의미한다.

• [1]: 은 결과값의 Shape를 의미하는데, 일종의 행, 열 등 차원의 수를 나타내는 값이다.
• 0: 최소값 0을 의미한다.
• 1: 최대값 1을 의미한다.

shape를 바꿔서 여러 개의 난수를 얻을 수 있다.

rand = tf.random.uniform([4], 0, 1)
print(rand)

tf.Tensor([0.8006196  0.61932623 0.3595978  0.6863916 ], shape=(4,), dtype=float32)

정규(normal) 분포를 통해서 난수를 얻을 수 있다. 정규 분포는 가운데가 높고 양극단으로 갈수록 낮아져서 종 모양을 그리는 분포를 말한다. 정규 분포의 난수를 구하기 위해서는 tf.random.uniform을 tf.random.normal로 바꾸기만 하면 된다.

rand = tf.random.normal([4], 0, 1)
print(rand)

tf.Tensor([-0.7653245  -1.318475   -0.0448174   0.06587371], shape=(4,), dtype=float32)

1 이상의 값도 나올 수 있고, 음수가 나올 수도 있는데, 여기서 두번째의 0은 정규분포의 평균을 말하고, 세번째의 1은 정규분포의 표준편차를 의미한다. 아래 소스코드를 통해서 균일분포와 정규분포의 차이점을 이해하기 바란다.

# Imports
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import warnings
warnings.simplefilter("ignore", UserWarning)

# Let's create an array of random numbers from uniform distribution
uniform = np.random.uniform(0,1,1000000)

# Let's create an array of random numbers from normal distribution
normal = np.random.normal(0,1,1000000)

# Let's plot them
ax = sns.distplot(uniform, label='Uniform Distribution')
bx = sns.distplot(normal, label= 'Normal Distribution')
legend = plt.legend()
plt.show()

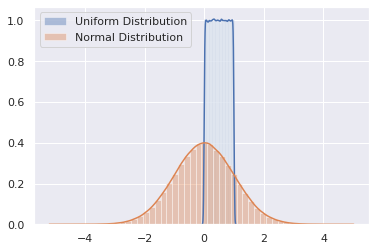
균일 분포와 정규 분포에 대해 각 100만개의 샘플을 구해서 히스토그램으로 나타내면 균일 분포는 최소값 0과 최대값 1 사이에서 균일하게 나타나지만, 정규분포는 평균 0을 기준으로 종형 곡선 (bell curve)를 그리게 되는 것을 확인할 수 있다.

정규 분포는 실생활에서 자주 볼 수 있는 분포 형태이며, 앞에서 소개한 Xavier 초기화나 He 초기화는 균일 분포와 정규 분포 중 하나를 택해서 신경망의 초기값을 만든다.

III. 뉴런 만들기

신경망의 가장 기본적인 구성요소인 뉴런을 만들어본다. 뉴런은 입력, 가중치, 활성화함수, 출력 등으로 구성된다. 뉴런에 대한 그림 설명은 본 교재 Page 40-41를 참고한다.

과거에는 뉴런을 퍼셉트론이라고 불렀으며, 입력을 받아서 계산 후 출력을 반환하는 단순한 구조였지만, 신경망은 이러한 뉴런이 여러 개가 모여 레이어(layer)를 구성한 후, 이 레이어가 다시 모여 구성된 형태를 띈다.

이 때의 뉴런은, 입력, 가중치, 활성화함수, 출력등으로 구성된다. 입력, 가중치, 출력은 보통 정수(integer)나 앞에서 살펴본 float 등이 많이 사용된다. 활성화함수는 뉴런의 출력값을 정하는 함수이며, 가장 간단한 형태의 뉴런은 입력에 가중치를 곱한 뒤 활성화함수를 취하면 출력을 얻을 수 있다.

뉴런에서 학습할 때 변하는 것은 가중치이다. 가중치는 처음에는 초기화를 통해 랜덤한 값을 넣고, 학습 과정에서 점차 일정한 값으로 수렴한다. 학습이 잘된다는 뜻의 의미는 좋은 가중치를 얻어서 원하는 출력값에 근접했다는 것을 의미한다.

이 때, 활성화함수가 사용되는데, 시그모이드(sigmoid), ReLU 등을 주로 쓰게 된다. 결론부터 말하면, 현재에는 시그모이드보다는 ReLU가 더 많이 쓰인다.

(1) 시그모이드(sigmoid)

시그모이드는 출력값을 0~1 사이로만 제한하지만, ReLU는 양수를 그대로 반환하기 때문에 값의 왜곡이 적어진다.

시그모이드 함수를 파이썬으로 구현해보자. 먼저 sigmoid() 구현한뒤 입력이 1일 때 기대출력이 0이 되는 뉴런을 만들어본다.

import math
def sigmoid(x): 
  return 1 / (1 + math.exp(-x))

x = 1
y = 0
w = tf.random.normal([1], 0, 1)
output = sigmoid(x * w)
print(output)

0.25820436275087716
-0.25820436275087716

각각의 코드에 대한 설명은 아래와 같다.

• x는 입력값을 의미
• y는 출력의 기대값을 의미
• w는 가중치로써, 정규분포의 랜덤한 값을 넣는다.
• output은 sigmoid() 함수에 입력과 가중치를 곱한 값을 넣어서 계산함

error = y - output
print(error)

-0.25820436275087716

실제 출력으로 나온 값은 0.25820436275087716이므로, 기대했던 0과는 오차가 발생함을 알 수가 있다. 여기서 뉴런이란 결국 w(즉, 가중치)값이며, 이제 이 가중치에 변화를 주어야 합니다. 대표적으로 가중치에 변화를 주는 것이 경사 하강법이며, 이것은 w(가중치)에 입력과 학습률(a)과 에러를 곱한 값을 더해주는 것이다. 학습률은 가중치(w)를 업데이트 하는 정도로 생각하면 된다.¹

w = w + x * a * error

경사 하강법이 효과를 발휘하는지 코드로 확인해보자.

for i in range(1000): 
  output = sigmoid(x * w)
  error = y - output
  w = w + x * 0.1 * error

  if i % 100 == 99:
    print(i, error, output)

99 -0.03173079700164497 0.03173079700164497
199 -0.024241452365306285 0.024241452365306285
299 -0.019590717239652087 0.019590717239652087
399 -0.016427360997418813 0.016427360997418813
499 -0.014138429413603958 0.014138429413603958
599 -0.012406450447051597 0.012406450447051597
699 -0.011050706128755142 0.011050706128755142
799 -0.00996094959269461 0.00996094959269461
899 -0.009066010254717002 0.009066010254717002
999 -0.008318118521116045 0.008318118521116045

기대값 0에 가까우려면 i = 99 보다는 i = 999가 더 0에 가까워지는 것을 확인할 수 있다.

IV. 연습 파일

• 구글 Colab에서 직접 연습해보자

V. Reference

김환희. (2020). 시작하세요! 텐서플로 2.0 프로그래밍: 기초 이론부터 실전 예제까지 한번에 끝내는 머신러닝, 딥러닝 핵심 가이드. 서울: 위키북스.