딥러닝 소개 - 심층 신경망 훈련하기
Page content
강의 홍보
- 취준생을 위한 강의를 제작하였습니다.
- 본 블로그를 통해서 강의를 수강하신 분은 게시글 제목과 링크를 수강하여 인프런 메시지를 통해 보내주시기를 바랍니다.
스타벅스 아이스 아메리카노를 선물로 보내드리겠습니다.
- [비전공자 대환영] 제로베이스도 쉽게 입문하는 파이썬 데이터 분석 - 캐글입문기
공지
-
본 Tutorial은 교재
핸즈온 머신러닝 2판를 활용하여 본 강사로부터 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다. -
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 분은 반드시 교재를 구매하실 것을 권해드립니다.
책 정말 좋습니다! 꼭 구매하세요!

개요
- 인경 신경망은(
Artificial Neural Network)을 촉발시킨 근원임- 뇌에 있는 생물학적 뉴런의 네트워크에서 영감을 받은 머신러닝 모델
- 활용예제
- 수백만개의 이미지 분류
- 수백만개의 비디어 추천
- 매우 복잡한 문제를 풀 때 유용한 머신러닝 모델
- Keras API
- 케라스는 신경망 구축, 훈련, 평가, 실행을 목적으로 설계된 API이자, 프레임워크
(1) 주요 환경 설정
- 주요 환경 설정은 아래와 같이 정의합니다.
# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)
# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"
# 텐서플로 ≥2.0 필수
import tensorflow as tf
assert tf.__version__ >= "2.0"
from tensorflow import keras
# 공통 모듈 임포트
import numpy as np
import pandas as pd
import os
# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)
# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("그림 저장:", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# 불필요한 경고를 무시합니다 (사이파이 이슈 #5998 참조)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
I. 그레이디언트 소실과 폭주
- 소실: 경사 하강법이 하위층의 연결 가중치를 변경되지 않은 채로 둔다면 안타깝게도 훈련이 좋은 솔루션으로 수렴되지 않음.
- 폭주: 그레이디언트가 점점 커져서 여러 층이 비정상적으로 큰 가중치로 갱신되면 알고리즘은 발산함. (보통 순환 신경망에서 나타남)
- 이렇게 불안정한 그레이디언트는 심층 신경망 훈련을 어렵게 만듬
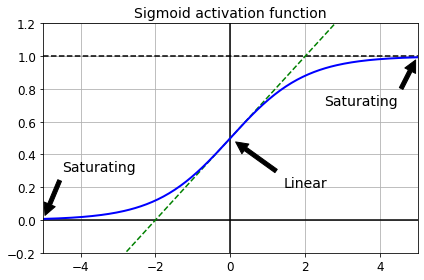
- 근본적인 원인은 로지스틱 활성화와 가중치 초기화 방법(정규분포)의 조합으로 진행 시, 복잡한 모형에서 출력의 분산이 입력의 분산보다 커짐을 확인
def logit(z):
return 1 / (1 + np.exp(-z))
z = np.linspace(-5, 5, 200)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [1, 1], 'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot([-5, 5], [-3/4, 7/4], 'g--')
plt.plot(z, logit(z), "b-", linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha="center")
plt.grid(True)
plt.title("Sigmoid activation function", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("sigmoid_saturation_plot")
plt.show()
그림 저장: sigmoid_saturation_plot
II. 불안정한 그레이디언트 문제를 해결하는 방법
- 크게 3가지의 초기화 방법이 나옴
- 자세한 설명은
교재 413~415 페이지참고 바람
- 자세한 설명은
| 초기화전략 | 활성화 함수 | $\sigma^2$ (정규분포) |
|---|---|---|
| 글로럿 | 없음. 탄젠트, 로지스틱, 소프트맥스 | 1 / $fan_{avg}$ |
| He | ReLU 함수와 그 변종들 |
2 / $fan_{in}$ |
| 르쿤 | SELU | 1 / $fan_{in}$ |
- 케라스는 기본적으로 글로럿 초기화 사용
keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")
- $fan_{in}$ 대신 $fan_{out}$ 기반의 균등분포
He초기화를 사용하고 싶다면 다음과 같이Variance Scaling을 사용할 수 있다.
he_avg_init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg', distribution='uniform')
keras.layers.Dense(10, activation="relu", kernel_initializer=he_avg_init)
III. 수렴하지 않는 활성화 함수
- 2010년 논문에서, 글로럿과 벤지오는 활성화 함수를 잘못 사용하면 그레이디언트의 소실이나 폭주로 이어질 수 있음
- 안타깝게도
ReLU함수는 완벽하지 않음- 훈련하는 동안 일부 뉴런이 0 이외의 값을 출력하지 않는다는 의미에서 죽었다고 말함
- 이를 보완하기 위해 다양한
ReLU함수의 변종이 존재- LeakyReLU
- RReLU
- PReLU
- 그 외에,
ELU,SELU활성화 함수도 있음 - 이를 다 외울 필요는 없다.
- 기본적으로는
SELU,ELU,LeakyReLU내에서 사용하는 것을 권함 - 각 활성화 함수의 특징 및 장단점은
교재 417~419 페이지 참조
(1) LeakyReLU를 활용한 모형 생성 및 평가
- 실전 예를 확인해보자.
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full / 255.0
X_test = X_test / 255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz
32768/29515 [=================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz
26427392/26421880 [==============================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz
8192/5148 [===============================================] - 0s 0us/step
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz
4423680/4422102 [==============================] - 0s 0us/step
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(),
keras.layers.Dense(100, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Epoch 1/10
1719/1719 [==============================] - 5s 3ms/step - loss: 1.2819 - accuracy: 0.6229 - val_loss: 0.8886 - val_accuracy: 0.7160
Epoch 2/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.7955 - accuracy: 0.7362 - val_loss: 0.7130 - val_accuracy: 0.7656
Epoch 3/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.6816 - accuracy: 0.7721 - val_loss: 0.6427 - val_accuracy: 0.7898
Epoch 4/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.6217 - accuracy: 0.7944 - val_loss: 0.5900 - val_accuracy: 0.8066
Epoch 5/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.5832 - accuracy: 0.8075 - val_loss: 0.5582 - val_accuracy: 0.8200
Epoch 6/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.5553 - accuracy: 0.8157 - val_loss: 0.5350 - val_accuracy: 0.8236
Epoch 7/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.5338 - accuracy: 0.8224 - val_loss: 0.5157 - val_accuracy: 0.8304
Epoch 8/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.5172 - accuracy: 0.8273 - val_loss: 0.5079 - val_accuracy: 0.8286
Epoch 9/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.5040 - accuracy: 0.8288 - val_loss: 0.4895 - val_accuracy: 0.8390
Epoch 10/10
1719/1719 [==============================] - 5s 3ms/step - loss: 0.4924 - accuracy: 0.8321 - val_loss: 0.4816 - val_accuracy: 0.8394
import pandas as pd
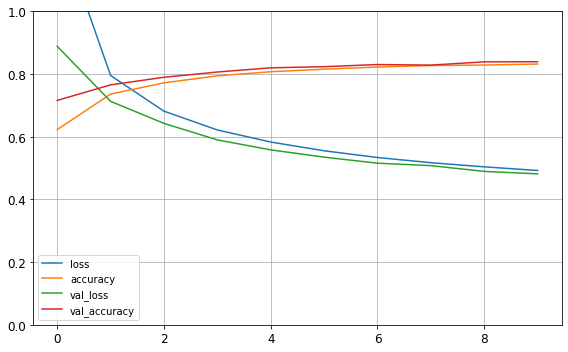
pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
save_fig("keras_learning_curves_plot")
plt.show()
그림 저장: keras_learning_curves_plot
model.evaluate(X_test, y_test)
313/313 [==============================] - 1s 2ms/step - loss: 0.5155 - accuracy: 0.8241
[0.5154786705970764, 0.8241000175476074]
IV. 배치 정규화
- 배치 정규화 (
Batch Normalization(BN)) 기법을 제안함- 마찬가지로 폭주 문제를 크게 감소시킬 수 있는 대안으로 제안됨
- 이 기법은 다음과 같이 작동됨
- 이 작업을 할 때에는 각 층에서 활성화 함수를 통과하기 전이나 후에 모델에 연산을 하나 추가함.
- 이 연산은 단순하게 입력을 원점에 맞추고 정규화한 다음, 각 층에서 두개의 새로운 파라미터로 결과값의 스케일을 조정하고 이동시킴.
- 즉, 하나는 스케일 조정, 다른 하나는 이동에 사용됨
- 많은 경우, 훈련 세트를 표준화할 필요는 없음
(1) 케라스로 배치 정규화 구현하기 (활성화 함수 이후)
- 은닉층의 활성화 함수 전이나 후에
BatchNormalization층을 추가하면 됨 - 아래 예제는 활성화 함수 이후에 배치 정규화 층을 추가하는 것임
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
model.summary()
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_1 (Flatten) (None, 784) 0
_________________________________________________________________
batch_normalization (BatchNo (None, 784) 3136
_________________________________________________________________
dense_3 (Dense) (None, 300) 235500
_________________________________________________________________
batch_normalization_1 (Batch (None, 300) 1200
_________________________________________________________________
dense_4 (Dense) (None, 100) 30100
_________________________________________________________________
batch_normalization_2 (Batch (None, 100) 400
_________________________________________________________________
dense_5 (Dense) (None, 10) 1010
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
_________________________________________________________________
- 모델에서 훈련되지 않는
2,368은 역전파로 학습되지 않는다는 뜻이다.
bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]
[('batch_normalization/gamma:0', True),
('batch_normalization/beta:0', True),
('batch_normalization/moving_mean:0', False),
('batch_normalization/moving_variance:0', False)]
- 첫번째 배치 정규화 층의 파라미터를 보면, 두 개는 (역전파로) 훈련되고 두 개는 훈련되지 않는다.
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Epoch 1/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.8293 - accuracy: 0.7221 - val_loss: 0.5539 - val_accuracy: 0.8160
Epoch 2/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.5703 - accuracy: 0.8036 - val_loss: 0.4792 - val_accuracy: 0.8380
Epoch 3/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.5161 - accuracy: 0.8213 - val_loss: 0.4424 - val_accuracy: 0.8490
Epoch 4/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4789 - accuracy: 0.8314 - val_loss: 0.4212 - val_accuracy: 0.8570
Epoch 5/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4548 - accuracy: 0.8407 - val_loss: 0.4051 - val_accuracy: 0.8616
Epoch 6/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.4387 - accuracy: 0.8445 - val_loss: 0.3931 - val_accuracy: 0.8632
Epoch 7/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4255 - accuracy: 0.8502 - val_loss: 0.3829 - val_accuracy: 0.8638
Epoch 8/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4124 - accuracy: 0.8538 - val_loss: 0.3759 - val_accuracy: 0.8664
Epoch 9/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.4027 - accuracy: 0.8583 - val_loss: 0.3691 - val_accuracy: 0.8676
Epoch 10/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.3925 - accuracy: 0.8613 - val_loss: 0.3630 - val_accuracy: 0.8664
model.evaluate(X_test, y_test)
313/313 [==============================] - 1s 2ms/step - loss: 0.3969 - accuracy: 0.8568
[0.39694663882255554, 0.8568000197410583]
(2) 케라스로 배치 정규화 구현하기 (활성화 함수 이전)
- 이번에는 활성화 함수 이전에 배치 정규화를 지정한다.
- 배치 정규화 층은 입력마다 이동 파라미터를 포함하기 때문에 이전 층에서 편향을 뺄 수 있음
- 층을 만들 때
use_bias=False로 설정
- 층을 만들 때
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
Epoch 1/10
1719/1719 [==============================] - 8s 5ms/step - loss: 1.0346 - accuracy: 0.6739 - val_loss: 0.6680 - val_accuracy: 0.7886
Epoch 2/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.6757 - accuracy: 0.7818 - val_loss: 0.5537 - val_accuracy: 0.8212
Epoch 3/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.5961 - accuracy: 0.8021 - val_loss: 0.4996 - val_accuracy: 0.8350
Epoch 4/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.5456 - accuracy: 0.8175 - val_loss: 0.4655 - val_accuracy: 0.8460
Epoch 5/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.5140 - accuracy: 0.8249 - val_loss: 0.4420 - val_accuracy: 0.8508
Epoch 6/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4915 - accuracy: 0.8309 - val_loss: 0.4238 - val_accuracy: 0.8538
Epoch 7/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.4742 - accuracy: 0.8375 - val_loss: 0.4103 - val_accuracy: 0.8582
Epoch 8/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4603 - accuracy: 0.8407 - val_loss: 0.3994 - val_accuracy: 0.8620
Epoch 9/10
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4466 - accuracy: 0.8459 - val_loss: 0.3911 - val_accuracy: 0.8640
Epoch 10/10
1719/1719 [==============================] - 8s 5ms/step - loss: 0.4338 - accuracy: 0.8500 - val_loss: 0.3828 - val_accuracy: 0.8680
model.evaluate(X_test, y_test)
313/313 [==============================] - 1s 2ms/step - loss: 0.4244 - accuracy: 0.8471
[0.42444711923599243, 0.847100019454956]
V. 사전훈련된 층 재사용하기
- 아주 큰 규모의
DNN을 처음부터 새로 훈련하는 것은 좋은 생각이 아님. - 신경망의 하위층을 재사용하는 것이 좋음
- 이를 전이 학습(
Transfer Learning)이라고 함.
- 이를 전이 학습(
- 상황 가정
- 샌들과 셔츠를 제외한 8개의 클래스는 분류하는
모델 A를 만들었고, 약 90% 정확도를 얻었다. - 이 때, 샌들과 셔츠 이미지를 구분하는 이진 분류기
모델 B를 만들었고, 약 97%의 정확도를 얻었다. - 이 때, 더 좋은 성능을 얻기 위해 어떻게 해야 할까?
- 샌들과 셔츠를 제외한 8개의 클래스는 분류하는
(1) 사전 훈련 개요
- 패션 MNIST 훈련 세트를 두 개로 나누어 본다.
X_train_A: 샌달과 셔츠(클래스 5와 6)을 제외한 모든 이미지X_train_B: 샌달과 셔츠 이미지 중 처음 200개만 가진 작은 훈련 세트
- 검증 세트와 테스트 세트도 이렇게 나눈다. 하지만 이미지 개수는 제한하지 않는다.
- A 세트(8개의 클래스를 가진 분류 문제)에서 모델을 훈련하고 이를 재사용하여 B 세트(이진 분류)를 해결해 본다.
- A 작업에서 B 작업으로 약간의 지식이 전달되기를 기대한다. 왜냐하면 A 세트의 클래스(스니커즈, 앵클 부츠, 코트, 티셔츠 등)가 B 세트에 있는 클래스(샌달과 셔츠)와 조금 비슷하기 때문이다.
- 하지만
Dense층을 사용하기 때문에 동일한 위치에 나타난 패턴만 재사용할 수 있다(반대로 합성곱 층은 훨씬 많은 정보를 전송한다). - 학습한 패턴을 이미지의 어느 위치에서나 감지할 수 있기 때문이다. CNN 장에서 자세히 알아 본다.
(2) 데이터셋 분리
- 샌달과 셔츠를 기준으로 데이터를 분리 하는 코드를 작성한다.
def split_dataset(X, y):
y_5_or_6 = (y == 5) | (y == 6) # 샌달 or 셔츠
y_A = y[~y_5_or_6]
y_A[y_A > 6] -= 2 # class [7, 8, 9]를 [5, 6, 7]로 이동
y_B = (y[y_5_or_6] == 6).astype(np.float32) # 이진 분류 task: 셔츠인가 (class 6)?
return ((X[~y_5_or_6], y_A),
(X[y_5_or_6], y_B))
(X_train_A, y_train_A), (X_train_B, y_train_B) = split_dataset(X_train, y_train)
(X_valid_A, y_valid_A), (X_valid_B, y_valid_B) = split_dataset(X_valid, y_valid)
(X_test_A, y_test_A), (X_test_B, y_test_B) = split_dataset(X_test, y_test)
X_train_B = X_train_B[:200]
y_train_B = y_train_B[:200]
- 분리가 완료되면, 데이터의 크기를 확인해본다.
X_train_A.shape
(43986, 28, 28)
X_train_B.shape
(200, 28, 28)
y_train_A[:30]
array([4, 0, 5, 7, 7, 7, 4, 4, 3, 4, 0, 1, 6, 3, 4, 3, 2, 6, 5, 3, 4, 5,
1, 3, 4, 2, 0, 6, 7, 1], dtype=uint8)
y_train_B[:30]
array([1., 1., 0., 0., 0., 0., 1., 1., 1., 0., 0., 1., 1., 0., 0., 0., 0.,
0., 0., 1., 1., 0., 0., 1., 1., 0., 1., 1., 1., 1.], dtype=float32)
- 실험 재현성을 위한 코드를 작성한다.
tf.random.set_seed(42)
np.random.seed(42)
(3) A 모형 생성 및 학습
- 초기 모형을 만든다.
- 모형을 학습한 후, 저장한다.
(my_model_A.h5)- H5 파일은
Hierarchical Data Format (HDF) - H5 파일은 항공 우주, 물리학, 공학, 금융, 학술 연구, 유전체학, 천문학, 전자 기기 및 의료 분야에서 주로 사용된다.
- H5 파일은
model_A = keras.models.Sequential()
model_A.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_A.add(keras.layers.Dense(n_hidden, activation="selu"))
model_A.add(keras.layers.Dense(8, activation="softmax"))
model_A.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_A.fit(X_train_A, y_train_A, epochs=20,
validation_data=(X_valid_A, y_valid_A))
Epoch 1/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.5926 - accuracy: 0.8103 - val_loss: 0.3890 - val_accuracy: 0.8677
Epoch 2/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.3523 - accuracy: 0.8786 - val_loss: 0.3289 - val_accuracy: 0.8824
Epoch 3/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.3170 - accuracy: 0.8895 - val_loss: 0.3013 - val_accuracy: 0.8991
Epoch 4/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2972 - accuracy: 0.8974 - val_loss: 0.2892 - val_accuracy: 0.9013
Epoch 5/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2834 - accuracy: 0.9022 - val_loss: 0.2774 - val_accuracy: 0.9066
Epoch 6/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2729 - accuracy: 0.9063 - val_loss: 0.2733 - val_accuracy: 0.9071
Epoch 7/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2641 - accuracy: 0.9092 - val_loss: 0.2720 - val_accuracy: 0.9091
Epoch 8/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2572 - accuracy: 0.9125 - val_loss: 0.2589 - val_accuracy: 0.9141
Epoch 9/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2518 - accuracy: 0.9135 - val_loss: 0.2562 - val_accuracy: 0.9143
Epoch 10/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2468 - accuracy: 0.9154 - val_loss: 0.2540 - val_accuracy: 0.9165
Epoch 11/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2422 - accuracy: 0.9178 - val_loss: 0.2494 - val_accuracy: 0.9155
Epoch 12/20
1375/1375 [==============================] - 5s 3ms/step - loss: 0.2382 - accuracy: 0.9188 - val_loss: 0.2511 - val_accuracy: 0.9128
Epoch 13/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2350 - accuracy: 0.9197 - val_loss: 0.2446 - val_accuracy: 0.9163
Epoch 14/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2315 - accuracy: 0.9213 - val_loss: 0.2413 - val_accuracy: 0.9178
Epoch 15/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2287 - accuracy: 0.9214 - val_loss: 0.2446 - val_accuracy: 0.9193
Epoch 16/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2254 - accuracy: 0.9224 - val_loss: 0.2386 - val_accuracy: 0.9195
Epoch 17/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2230 - accuracy: 0.9232 - val_loss: 0.2405 - val_accuracy: 0.9175
Epoch 18/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2201 - accuracy: 0.9243 - val_loss: 0.2429 - val_accuracy: 0.9158
Epoch 19/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2178 - accuracy: 0.9251 - val_loss: 0.2328 - val_accuracy: 0.9205
Epoch 20/20
1375/1375 [==============================] - 4s 3ms/step - loss: 0.2156 - accuracy: 0.9262 - val_loss: 0.2332 - val_accuracy: 0.9208
model_A.save("my_model_A.h5")
(4) B 모형 생성 및 학습
- 이제 B 모형을 생성하고 학습해본다.
model_B = keras.models.Sequential()
model_B.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_B.add(keras.layers.Dense(n_hidden, activation="selu"))
model_B.add(keras.layers.Dense(1, activation="sigmoid"))
model_B.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B.fit(X_train_B, y_train_B, epochs=20,
validation_data=(X_valid_B, y_valid_B))
Epoch 1/20
7/7 [==============================] - 0s 27ms/step - loss: 0.9573 - accuracy: 0.4650 - val_loss: 0.6314 - val_accuracy: 0.6004
Epoch 2/20
7/7 [==============================] - 0s 14ms/step - loss: 0.5692 - accuracy: 0.7450 - val_loss: 0.4784 - val_accuracy: 0.8529
Epoch 3/20
7/7 [==============================] - 0s 14ms/step - loss: 0.4503 - accuracy: 0.8650 - val_loss: 0.4102 - val_accuracy: 0.8945
Epoch 4/20
7/7 [==============================] - 0s 14ms/step - loss: 0.3879 - accuracy: 0.8950 - val_loss: 0.3647 - val_accuracy: 0.9178
Epoch 5/20
7/7 [==============================] - 0s 13ms/step - loss: 0.3435 - accuracy: 0.9250 - val_loss: 0.3300 - val_accuracy: 0.9320
Epoch 6/20
7/7 [==============================] - 0s 13ms/step - loss: 0.3081 - accuracy: 0.9300 - val_loss: 0.3019 - val_accuracy: 0.9402
Epoch 7/20
7/7 [==============================] - 0s 14ms/step - loss: 0.2800 - accuracy: 0.9350 - val_loss: 0.2804 - val_accuracy: 0.9422
Epoch 8/20
7/7 [==============================] - 0s 14ms/step - loss: 0.2564 - accuracy: 0.9450 - val_loss: 0.2606 - val_accuracy: 0.9473
Epoch 9/20
7/7 [==============================] - 0s 14ms/step - loss: 0.2362 - accuracy: 0.9550 - val_loss: 0.2428 - val_accuracy: 0.9523
Epoch 10/20
7/7 [==============================] - 0s 14ms/step - loss: 0.2188 - accuracy: 0.9600 - val_loss: 0.2281 - val_accuracy: 0.9544
Epoch 11/20
7/7 [==============================] - 0s 15ms/step - loss: 0.2036 - accuracy: 0.9700 - val_loss: 0.2150 - val_accuracy: 0.9584
Epoch 12/20
7/7 [==============================] - 0s 14ms/step - loss: 0.1898 - accuracy: 0.9700 - val_loss: 0.2036 - val_accuracy: 0.9584
Epoch 13/20
7/7 [==============================] - 0s 15ms/step - loss: 0.1773 - accuracy: 0.9750 - val_loss: 0.1931 - val_accuracy: 0.9615
Epoch 14/20
7/7 [==============================] - 0s 14ms/step - loss: 0.1668 - accuracy: 0.9800 - val_loss: 0.1838 - val_accuracy: 0.9635
Epoch 15/20
7/7 [==============================] - 0s 15ms/step - loss: 0.1570 - accuracy: 0.9900 - val_loss: 0.1746 - val_accuracy: 0.9686
Epoch 16/20
7/7 [==============================] - 0s 16ms/step - loss: 0.1481 - accuracy: 0.9900 - val_loss: 0.1674 - val_accuracy: 0.9686
Epoch 17/20
7/7 [==============================] - 0s 14ms/step - loss: 0.1406 - accuracy: 0.9900 - val_loss: 0.1604 - val_accuracy: 0.9706
Epoch 18/20
7/7 [==============================] - 0s 15ms/step - loss: 0.1334 - accuracy: 0.9900 - val_loss: 0.1539 - val_accuracy: 0.9706
Epoch 19/20
7/7 [==============================] - 0s 14ms/step - loss: 0.1268 - accuracy: 0.9900 - val_loss: 0.1482 - val_accuracy: 0.9716
Epoch 20/20
7/7 [==============================] - 0s 15ms/step - loss: 0.1208 - accuracy: 0.9900 - val_loss: 0.1431 - val_accuracy: 0.9716
(5) 케라스를 사용한 전이 학습
- 먼저
모델 A를 로드하고 이 모델의 층을 기반으로 새로운 모델model_B_on_A를 만든다. - 출력층만 제외 하고 모든 층을 재사용한다.
model_A = keras.models.load_model("my_model_A.h5")
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))
model_A와model_B_on_A는 일부 층을 공유함.model_B_on_A훈련 시에는model_A도 영향을 받는다.- 이제
모델 B를 위해model_B_on_A를 훈련할 수 있다.- 그런데, 새로운 출력층이 초기화 되어 있으므로 큰 오차를 만든다.
- 이를 방지하기 위해, 처음 몇 번의 에포크 동안 재사용된 층을 동결하고, 새로운 층에게 적절한 가중치를 학습할 시간을 준다.
- 이 때, 모든 층의
trainable속성을False로 지정하고 모델을 컴파일 한다.
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
(6) 모형 학습
- 이제, 몇번의 에포크 동안 모형을 훈련할 수 있다.
- 그리고, 재사용된 층의 동결을 해제하고 모델을 다시 컴파일 한다.
모델 B에 맞게 재사용된 층을 세밀하게 튜닝하기 위해 훈련을 계속한다.
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True
model_B_on_A.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
validation_data=(X_valid_B, y_valid_B))
Epoch 1/4
7/7 [==============================] - 0s 25ms/step - loss: 0.5759 - accuracy: 0.6550 - val_loss: 0.5812 - val_accuracy: 0.6379
Epoch 2/4
7/7 [==============================] - 0s 12ms/step - loss: 0.5396 - accuracy: 0.6750 - val_loss: 0.5439 - val_accuracy: 0.6826
Epoch 3/4
7/7 [==============================] - 0s 13ms/step - loss: 0.5029 - accuracy: 0.7250 - val_loss: 0.5121 - val_accuracy: 0.7150
Epoch 4/4
7/7 [==============================] - 0s 13ms/step - loss: 0.4716 - accuracy: 0.7550 - val_loss: 0.4835 - val_accuracy: 0.7333
Epoch 1/16
7/7 [==============================] - 0s 27ms/step - loss: 0.3938 - accuracy: 0.8150 - val_loss: 0.3452 - val_accuracy: 0.8641
Epoch 2/16
7/7 [==============================] - 0s 13ms/step - loss: 0.2787 - accuracy: 0.9350 - val_loss: 0.2600 - val_accuracy: 0.9270
Epoch 3/16
7/7 [==============================] - 0s 14ms/step - loss: 0.2079 - accuracy: 0.9650 - val_loss: 0.2111 - val_accuracy: 0.9554
Epoch 4/16
7/7 [==============================] - 0s 14ms/step - loss: 0.1670 - accuracy: 0.9800 - val_loss: 0.1793 - val_accuracy: 0.9696
Epoch 5/16
7/7 [==============================] - 0s 14ms/step - loss: 0.1398 - accuracy: 0.9800 - val_loss: 0.1564 - val_accuracy: 0.9757
Epoch 6/16
7/7 [==============================] - 0s 14ms/step - loss: 0.1198 - accuracy: 0.9950 - val_loss: 0.1396 - val_accuracy: 0.9797
Epoch 7/16
7/7 [==============================] - 0s 15ms/step - loss: 0.1051 - accuracy: 0.9950 - val_loss: 0.1268 - val_accuracy: 0.9838
Epoch 8/16
7/7 [==============================] - 0s 15ms/step - loss: 0.0938 - accuracy: 0.9950 - val_loss: 0.1166 - val_accuracy: 0.9858
Epoch 9/16
7/7 [==============================] - 0s 16ms/step - loss: 0.0848 - accuracy: 1.0000 - val_loss: 0.1068 - val_accuracy: 0.9888
Epoch 10/16
7/7 [==============================] - 0s 14ms/step - loss: 0.0763 - accuracy: 1.0000 - val_loss: 0.1002 - val_accuracy: 0.9899
Epoch 11/16
7/7 [==============================] - 0s 16ms/step - loss: 0.0704 - accuracy: 1.0000 - val_loss: 0.0941 - val_accuracy: 0.9899
Epoch 12/16
7/7 [==============================] - 0s 15ms/step - loss: 0.0649 - accuracy: 1.0000 - val_loss: 0.0890 - val_accuracy: 0.9899
Epoch 13/16
7/7 [==============================] - 0s 15ms/step - loss: 0.0602 - accuracy: 1.0000 - val_loss: 0.0841 - val_accuracy: 0.9899
Epoch 14/16
7/7 [==============================] - 0s 14ms/step - loss: 0.0559 - accuracy: 1.0000 - val_loss: 0.0804 - val_accuracy: 0.9899
Epoch 15/16
7/7 [==============================] - 0s 14ms/step - loss: 0.0525 - accuracy: 1.0000 - val_loss: 0.0770 - val_accuracy: 0.9899
Epoch 16/16
7/7 [==============================] - 0s 13ms/step - loss: 0.0496 - accuracy: 1.0000 - val_loss: 0.0740 - val_accuracy: 0.9899
(7) 모형 평가
- 이제 최종 점수를 확인한다.
- 먼저
model_B의 성능을 확인한다.
model_B.evaluate(X_test_B, y_test_B)
63/63 [==============================] - 0s 2ms/step - loss: 0.1408 - accuracy: 0.9705
[0.14084088802337646, 0.9704999923706055]
- 그리고, 전이학습 모델의 성능을 확인한다.
model_B_on_A.evaluate(X_test_B, y_test_B)
63/63 [==============================] - 0s 2ms/step - loss: 0.0682 - accuracy: 0.9930
[0.06821806728839874, 0.9929999709129333]
- 모형의 성능이 크게 확산되었음을 확인 했다.
VI. 고속 옵티마이저
- 아주 큰 심층 신경망의 훈련 속도는 심각하게 느려짐
- 표준적인 경사 하강법 외의 다른 옵티마지어를 사용해본다.
- 옵티마이저의 종류는 여러가지가 있다.
- 모멘텀 최적화
- 네스테로프 가속 경사
- AdaGrad
- RMSProp
- Adam
- Nadam
- 각각의 특징은
교재 434~443을 확인한다. - 옵티마이저를 사용하는 이유는 훈련의 속도를 높이기 위한 것
(1) 벤치마킹
- 각각의
Optimizer의 성능을 비교하는 벤치마킹 코드를 작성한다.
from tensorflow import keras
from tensorflow.keras import datasets
import matplotlib.pylab as plt
import numpy as np
- mnist 데이터를 불러온 후 훈련데이터와 테스트데이터로 분리한다.
(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)
x_train = keras.utils.normalize(x_train, axis=1)
x_test = keras.utils.normalize(x_test, axis=1)
x_train.shape, y_train.shape, x_test.shape, y_test.shape
((60000, 28, 28), (60000, 10), (10000, 28, 28), (10000, 10))
- 데이터를 훈련시키는 함수를 작성한다.
def train_mnist(optimizer):
model = keras.Sequential([
keras.layers.Flatten(input_shape=x_train[0].shape),
keras.layers.Dense(250, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(
optimizer=optimizer,
loss=keras.losses.categorical_crossentropy,
metrics=['acc']
)
history = model.fit(x_train, y_train,
batch_size=128,
epochs=10,
verbose=False,
shuffle=True,
validation_data=(x_test, y_test))
return history, model
- 아래 코드는
optimizer종류에 따라 각각의 훈련 히스토리가 어떻게 변하는지 각각의List에 담았다.
mnist = {
'sgd': {'loss': [], 'acc': [], 'val_loss': [], 'val_acc': [], 'history': []},
'rmsprop': {'loss': [], 'acc': [], 'val_loss': [], 'val_acc': [], 'history': []},
'adagrad': {'loss': [], 'acc': [], 'val_loss': [], 'val_acc': [], 'history': []},
'adam': {'loss': [], 'acc': [], 'val_loss': [], 'val_acc': [], 'history': []}
}
for optimizer in ['sgd', 'rmsprop', 'adagrad', 'adam']:
print('--- {} ---'.format(optimizer))
for i in range(2):
print('starting ', i)
history, model = train_mnist(optimizer)
train_loss, train_accuracy = model.evaluate(x_train, y_train, verbose=False)
val_loss, val_accuracy = model.evaluate(x_test, y_test, verbose=False)
mnist[optimizer]['loss'].append(train_loss)
mnist[optimizer]['acc'].append(train_accuracy)
mnist[optimizer]['val_loss'].append(val_loss)
mnist[optimizer]['val_acc'].append(val_accuracy)
mnist[optimizer]['history'].append(history)
--- sgd ---
starting 0
starting 1
--- rmsprop ---
starting 0
starting 1
--- adagrad ---
starting 0
starting 1
--- adam ---
starting 0
starting 1
- 각 모형의 결과값을 출력하는 코드를 작성했다.
for opt in ['sgd', 'rmsprop', 'adagrad', 'adam']:
for key in ['acc', 'val_acc', 'loss', 'val_loss']:
print(opt, key, np.mean(mnist[opt][key]))
sgd acc 0.895841658115387
sgd val_acc 0.9036500155925751
sgd loss 0.37897732853889465
sgd val_loss 0.36478106677532196
rmsprop acc 0.9932583272457123
rmsprop val_acc 0.9764000177383423
rmsprop loss 0.02655513398349285
rmsprop val_loss 0.08304187655448914
adagrad acc 0.9117666780948639
adagrad val_acc 0.9156999886035919
adagrad loss 0.31952860951423645
adagrad val_loss 0.31258873641490936
adam acc 0.9960833191871643
adam val_acc 0.9763499796390533
adam loss 0.01956858392804861
adam val_loss 0.07723309472203255
- 실제 모형을 훈련시킬 때, 값을 시각화로 구현하여 과적합이 일어나는지 안 일어나는지 확인하는 코드를 작성했다.
- 또한, 각
Optimizer의 성능을 비교하는 그래프를 작성했다.
plt.figure(figsize=(20,4))
for i in range(4):
plt.subplot(1,4,i+1)
key = ['acc', 'val_acc', 'loss', 'val_loss'][i]
title = ['Training Accuracy on MNIST', 'Validation Accuracy on MNIST', 'Training Loss on MNIST', 'Validation Loss on MNIST'][i]
for opt in ['sgd', 'rmsprop', 'adagrad', 'adam']:
hist = np.zeros(10)
for h in mnist[opt]['history']:
hist += np.array(h.history[key])
mean = hist / 2 # range(2) 값과 대응 시킨다.
plt.plot(mean, label=opt)
plt.legend()
plt.title(title)
plt.plot()
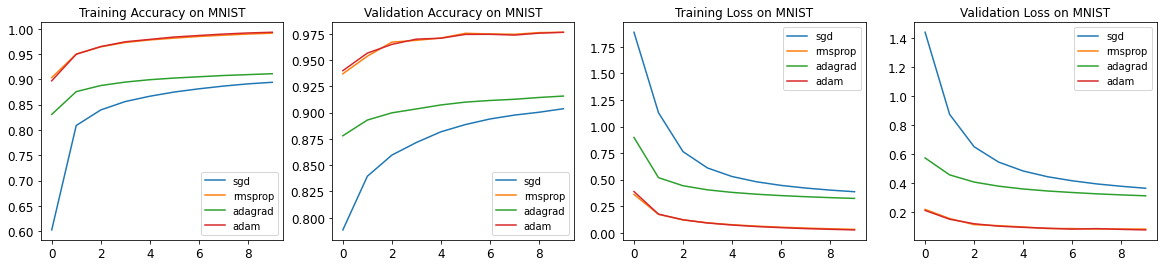
- 위 결과에서 보여주듯이,
Optimizer를 사용한다면Adam또는RMSProp를 우선 고려하는 것이 좋다.
VII. Reference
Wierenga, R. (2020, March 03). An Empirical Comparison of Optimizers for Machine Learning Models. Retrieved July 17, 2020, from https://heartbeat.fritz.ai/an-empirical-comparison-of-optimizers-for-machine-learning-models-b86f29957050
