딥러닝 소개 - 인공 신경망 소개

2020-07-15

Deep Learning, 딥러닝, Python

Page content

강의 홍보

취준생을 위한 강의를 제작하였습니다.
본 블로그를 통해서 강의를 수강하신 분은 게시글 제목과 링크를 수강하여 인프런 메시지를 통해 보내주시기를 바랍니다.
- 스타벅스 아이스 아메리카노를 선물로 보내드리겠습니다.
[비전공자 대환영] 제로베이스도 쉽게 입문하는 파이썬 데이터 분석 - 캐글입문기

공지

본 Tutorial은 교재 핸즈온 머신러닝 2판를 활용하여 본 강사로부터 국비교육 강의를 듣는 사람들에게 자료 제공을 목적으로 제작하였습니다.
강사의 주관적인 판단으로 압축해서 자료를 정리하였기 때문에, 자세하게 공부를 하고 싶은 분은 반드시 교재를 구매하실 것을 권해드립니다.

책 정말 좋습니다! 꼭 구매하세요!

개요

인경 신경망은(Artificial Neural Network)을 촉발시킨 근원임
- 뇌에 있는 생물학적 뉴런의 네트워크에서 영감을 받은 머신러닝 모델
활용예제
- 수백만개의 이미지 분류
- 수백만개의 비디어 추천
- 매우 복잡한 문제를 풀 때 유용한 머신러닝 모델
Keras API
- 케라스는 신경망 구축, 훈련, 평가, 실행을 목적으로 설계된 API이자, 프레임워크

(1) 주요 환경 설정

주요 환경 설정은 아래와 같이 정의합니다.

# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)

# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"

# 텐서플로 ≥2.0 필수
import tensorflow as tf
assert tf.__version__ >= "2.0"
from tensorflow import keras

# 공통 모듈 임포트
import numpy as np
import pandas as pd
import os

# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)

# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "ann"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)

def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
    path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
    print("그림 저장:", fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path, format=fig_extension, dpi=resolution)

# 불필요한 경고를 무시합니다 (사이파이 이슈 #5998 참조)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")

I. 퍼셉트론

1957년, 프랑크 로젠플라트가 제안
헤비사이드 계단 함수 (교재, P. 357)
- 입력의 선형 조합을 계산해 임계값을 기준으로 이진분류 (양성, 음성)
퍼셉트론은 층이 하나뿐인 TLU(Threshold Logic Unit)로 구성됨
- 모든 뉴런이 이전 층의 모든 뉴런과 연결되어 있을 때 완전 연결 층(Fully Connected Layer) 또는 밀집 층(Dense Layer)라고 부름

(1) 사이킷런 예제

Perceptron 클래스 제공
교재 360페이지에 있는 소스 코드보다 아래 소스 코드를 참고
사이킷런 향후 버전에서 max_iter와 tol 매개변수의 기본값이 바뀌기 때문에 경고를 피하기 위해 명시적으로 지정

import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron

iris = load_iris()
X = iris.data[:, (2, 3)]  # 꽃잎 길이, 꽃잎 너비
y = (iris.target == 0).astype(np.int)

per_clf = Perceptron(max_iter=1000, tol=1e-3, random_state=42)
per_clf.fit(X, y)

y_pred = per_clf.predict([[2, 0.5]])

y_pred

array([1])

(2) 다층 퍼셉트론

(1969년) 마빈 민스키와 시모어 페퍼트는 퍼셉트론의 여러가지 심각한 약점 언급, 특히 간단한 문제도 풀 수 없음 확인
- 참조: Tensorflow 2.0 Tutorial ch3.3.5 - 세번째 신경망 네트워크 - XOR
- 이 때, 퍼셉트론을 여러 개 쌓아올리면 일부 제약을 줄일 수 있음. 이를 다층 퍼셉트론(MLP)라고 부름
그러나, 다층 퍼셉트론을 훈련할 방법을 찾기 위해 노력했으나 성공하지 못함

(3) 역전파

교재 361페이지 참조
- 다층 퍼셉트론은 크게 입력-은닉-출력층으로 구성됨
- 은닉층을 여러개 쌓아 올린 인공 신경망을 심층 신경망(DNN)이라고 부름
딥러닝은 여러개를 쌓아 올리는 심층 신경망을 연구하는 분야임
1986년, 역전파 훈련 알고리즘 소개하는 논문 공개(by 데이비드 루멜하트, 제프리 힌턴, 로날드 윌리엄스)
- 그레이디언트를 자동으로 계산(자동 미분)하는 경사 하강법
- 네트워크를 두번 통과함 (정방향, 역방향)
- 목적은 오차를 감소시키기 위해 각 연결 가중치와 편향값이 어떻게 바뀌어야 할지 알 수 있음

(4) 활성화 함수

경사 하강법이 잘 작동할 수 있도록 다층 퍼셉트론 구조에 중요한 변화를 주는데, 이를 활성화 함수라 함
활성화 함수의 주 목적은, 문제 해결을 위해 도입된 것
- 선형 변환을 해도 비선형 문제는 해결하지 못함, (예: 선형회귀와 로지스틱회귀의 차이점)
- 선형변환에 비선형을 주는 것이 활성화 함수이며, 다만 어떻게 줄 것인지에 따라 종류가 나눠짐

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def relu(z):
    return np.maximum(0, z)

def derivative(f, z, eps=0.000001):
    return (f(z + eps) - f(z - eps))/(2 * eps)

z = np.linspace(-5, 5, 200)

plt.figure(figsize=(11,4))

plt.subplot(121)
plt.plot(z, np.sign(z), "r-", linewidth=1, label="Step")
plt.plot(z, sigmoid(z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, np.tanh(z), "b-", linewidth=2, label="Tanh")
plt.plot(z, relu(z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
plt.legend(loc="center right", fontsize=14)
plt.title("Activation functions", fontsize=14)
plt.axis([-5, 5, -1.2, 1.2])

plt.subplot(122)
plt.plot(z, derivative(np.sign, z), "r-", linewidth=1, label="Step")
plt.plot(0, 0, "ro", markersize=5)
plt.plot(0, 0, "rx", markersize=10)
plt.plot(z, derivative(sigmoid, z), "g--", linewidth=2, label="Sigmoid")
plt.plot(z, derivative(np.tanh, z), "b-", linewidth=2, label="Tanh")
plt.plot(z, derivative(relu, z), "m-.", linewidth=2, label="ReLU")
plt.grid(True)
#plt.legend(loc="center right", fontsize=14)
plt.title("Derivatives", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])

save_fig("activation_functions_plot")
plt.show()

그림 저장: activation_functions_plot

png

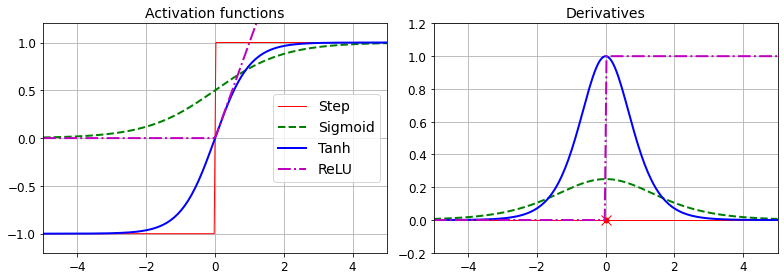
하이퍼폴릭 탄젠트 함수: $tanh(z)=2\sigma(2z)-1$. 로지스틱 함수와 같은 0~1 사이이고, 출력 범위는 -1~1 사이임
ReLU 함수: $ReLU(z)=max(0,z)$. 연속적이지만, $z=0$에서 미분 가능하지 않음. $z<0$일 경우에는 0이다. 그러나, 실제로 잘 작동하고 계산 속도가 빠르다는 장점이 있어 기본 활성화 함수가 됨.

II. 회귀를 위한 다층 퍼셉트론(MLP)

회귀 모형에 적용 가능, 이 때에는 출력 뉴런이 하나만 필요함
뉴런의 출력값이 예측값임.
회귀 MLP의 구조는 아래와 같음

하이퍼파라미터	일반적인 값
입력 뉴런 수	특성마다 하나
은닉층 수	문제에 따라 다름 (1~5)
은닉층의 뉴런 수	문제에 따라 다름 (10~100)
출력 뉴런 수	예측 차원마다 하나
은닉층의 활성화 함수	주로 ReLU
출력층의 활성화 함수	없음. 또는 출력이 양수일 때, ReLU/softplus
손실 함수	MSE

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

housing = fetch_california_housing()

X_train_full, X_test, y_train_full, y_test = train_test_split(housing.data, housing.target, random_state=42)
X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full, random_state=42)

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
X_test = scaler.transform(X_test)

np.random.seed(42)
tf.random.set_seed(42)

model = keras.models.Sequential([
    keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]),
    keras.layers.Dense(1)
])
model.compile(loss="mean_squared_error", optimizer=keras.optimizers.SGD(lr=1e-3))
history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid))
mse_test = model.evaluate(X_test, y_test)
X_new = X_test[:3]
y_pred = model.predict(X_new)

Epoch 1/20
363/363 [==============================] - 1s 2ms/step - loss: 1.6419 - val_loss: 0.8560
Epoch 2/20
363/363 [==============================] - 1s 2ms/step - loss: 0.7047 - val_loss: 0.6531
Epoch 3/20
363/363 [==============================] - 1s 2ms/step - loss: 0.6345 - val_loss: 0.6099
Epoch 4/20
363/363 [==============================] - 1s 2ms/step - loss: 0.5977 - val_loss: 0.5658
Epoch 5/20
363/363 [==============================] - 1s 2ms/step - loss: 0.5706 - val_loss: 0.5355
Epoch 6/20
363/363 [==============================] - 1s 2ms/step - loss: 0.5472 - val_loss: 0.5173
Epoch 7/20
363/363 [==============================] - 1s 2ms/step - loss: 0.5288 - val_loss: 0.5081
Epoch 8/20
363/363 [==============================] - 1s 2ms/step - loss: 0.5130 - val_loss: 0.4799
Epoch 9/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4992 - val_loss: 0.4690
Epoch 10/20
363/363 [==============================] - 1s 1ms/step - loss: 0.4875 - val_loss: 0.4656
Epoch 11/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4777 - val_loss: 0.4482
Epoch 12/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4688 - val_loss: 0.4479
Epoch 13/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4615 - val_loss: 0.4296
Epoch 14/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4547 - val_loss: 0.4233
Epoch 15/20
363/363 [==============================] - 1s 1ms/step - loss: 0.4488 - val_loss: 0.4176
Epoch 16/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4435 - val_loss: 0.4123
Epoch 17/20
363/363 [==============================] - 1s 1ms/step - loss: 0.4389 - val_loss: 0.4071
Epoch 18/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4347 - val_loss: 0.4037
Epoch 19/20
363/363 [==============================] - 1s 2ms/step - loss: 0.4306 - val_loss: 0.4000
Epoch 20/20
363/363 [==============================] - 1s 1ms/step - loss: 0.4273 - val_loss: 0.3969
162/162 [==============================] - 0s 964us/step - loss: 0.4212

모형의 그래프를 그려본다.

plt.plot(pd.DataFrame(history.history))
plt.grid(True)
plt.gca().set_ylim(0, 1)
plt.show()

png

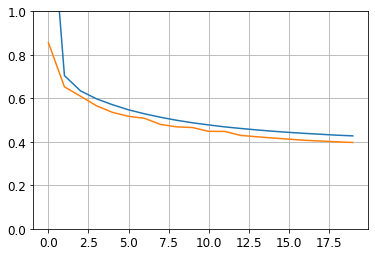
마지막으로 예측값을 적용한다.

y_pred

array([[0.38856643],
       [1.6792021 ],
       [3.1022794 ]], dtype=float32)

III. 분류를 위한 다층 퍼셉트론(MLP)

이진 분류 문제는 로지스틱 활성화 함수를 가진 하나의 출력 뉴런만 필요
다층 퍼셉트론은 다중 레이블 이진 분류 문제를 쉽게 처리할 수 있도록 함
- 이 때, 두개의 출력 뉴런이 필요
- 만약, 다중분류이면, 다중분류의 숫자만큼 출력 뉴런이 필요함
분류 MLP의 전형적인 구조는 다음과 같다.

하이퍼파라미터	이진분류	다중 레이블 분류	다중 분류
입력층과 은닉층	회귀와 동일	회귀와 동일	회귀와 동일
출력 뉴런 수	1개	레이블마다 1개	클래스마다 1개
출력층의 활성화 함수	로지스틱 함수	로지스틱 함수	소프트맥스 함수
손실함수	크로스 엔트로피	크로스 엔트로피	크로스 엔트로피

(1) 모듈 불러오기

모듈을 불러옵니다.

import tensorflow as tf
from tensorflow import keras

print(tf.__version__)
print(keras.__version__)

2.2.0
2.3.0-tf

(2) 데이터 불러오기

Fashion MNIST를 불러옵니다.

fashion_mnist = keras.datasets.fashion_mnist
(X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data()

이미지의 크기는 28 x 28크기의 배열이다.
또한 픽셀 강도가 실수(0.0에서 255.0까지)가 아니라 정수(0에서 255까지)로 표현되어 있다.

print(X_train_full.shape)
print(X_train_full.dtype)

(60000, 28, 28)
uint8

(3) 데이터셋 분리

훈련데이터와 테스트 데이터로 분리합니다.
간편하게 픽셀 강도를 255.0으로 나누너 0~1 사이 범위로 조정함.

X_valid, X_train = X_train_full[:5000] / 255., X_train_full[5000:] / 255.
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
X_test = X_test / 255.

이제 예측하려는 레이블을 확인해보자.

y_train

array([4, 0, 7, ..., 3, 0, 5], dtype=uint8)

각 단계별 레이블 이름을 다음과 같이 정의한다.

class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat",
               "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]

훈련 세트에 있는 첫번째 이미지 이름은 코트이다.

class_names[y_train[0]]

'Coat'

모형 학습 전, 데이터세트의 크기가 동일한지 확인한다.

print(X_valid.shape)
print(X_test.shape)

(5000, 28, 28)
(10000, 28, 28)

위 28, 28이 다르면 모형 예측이 되지 않는다.

(4) 데이터 시각화

시각화를 통해, 실제 이미지가 어떻게 생겼는지 확인해본다.

plt.imshow(X_train[0], cmap="binary")
plt.axis('off')
plt.show()

png

조금 더 자세하게 데이터를 출력해보자.

n_rows = 4
n_cols = 10
plt.figure(figsize=(n_cols * 1.2, n_rows * 1.2))
for row in range(n_rows):
    for col in range(n_cols):
        index = n_cols * row + col
        plt.subplot(n_rows, n_cols, index + 1)
        plt.imshow(X_train[index], cmap="binary", interpolation="nearest")
        plt.axis('off')
        plt.title(class_names[y_train[index]], fontsize=12)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('fashion_mnist_plot', tight_layout=False)
plt.show()

그림 저장: fashion_mnist_plot

png

(5) 모형 만들기

이제 신경망 모형을 만든다.

model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))

위 모형에 대한 구체적인 설명은 교재 373 페이지를 확인한다.

keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)

코드는 일종의 실험 재현성을 위한 코드이다.

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dense(300, activation="relu"),
    keras.layers.Dense(100, activation="relu"),
    keras.layers.Dense(10, activation="softmax")
])

summary()메서드는 모델에 있는 모든 층을 출력함

model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten (Flatten)            (None, 784)               0         
_________________________________________________________________
dense (Dense)                (None, 300)               235500    
_________________________________________________________________
dense_1 (Dense)              (None, 100)               30100     
_________________________________________________________________
dense_2 (Dense)              (None, 10)                1010      
=================================================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0
_________________________________________________________________

모형이 만들어가지는 과정을 출력할 수 있다.

keras.utils.plot_model(model, "my_fashion_mnist_model.png", show_shapes=True)

png

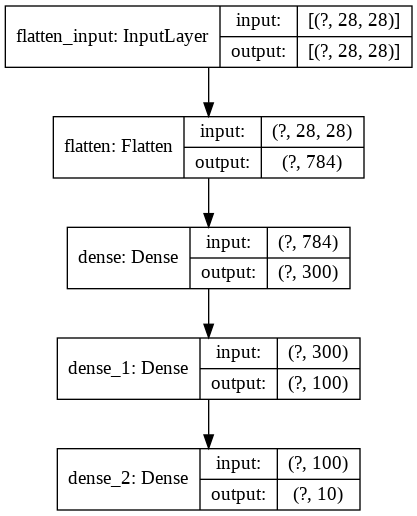
(6) 모델 컴파일

모델을 만들고 나서 compile() 메서드를 호출하여 사용할 손실 함수와 옵티마이저(optimizer)를 지정한다.

model.compile(loss="sparse_categorical_crossentropy",
              optimizer="sgd",
              metrics=["accuracy"])

위 모형에 대한 구체적인 설명은 교재 377페이지를 참고한다.

(7) 모델 훈련

케라스는 에포크 횟수를 전달함
에포크가 끝날 때 마다 검증 세트를 사용해 손실과 추가적인 측정 지표를 계산

history = model.fit(X_train, y_train, epochs=30,
                    validation_data=(X_valid, y_valid))

Epoch 1/30
1719/1719 [==============================] - 7s 4ms/step - loss: 0.7237 - accuracy: 0.7643 - val_loss: 0.5213 - val_accuracy: 0.8226
Epoch 2/30
1719/1719 [==============================] - 8s 4ms/step - loss: 0.4842 - accuracy: 0.8318 - val_loss: 0.4353 - val_accuracy: 0.8526
Epoch 3/30
1719/1719 [==============================] - 8s 5ms/step - loss: 0.4391 - accuracy: 0.8458 - val_loss: 0.5304 - val_accuracy: 0.7996
Epoch 4/30
1719/1719 [==============================] - 8s 5ms/step - loss: 0.4123 - accuracy: 0.8566 - val_loss: 0.3916 - val_accuracy: 0.8650
Epoch 5/30
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3939 - accuracy: 0.8622 - val_loss: 0.3745 - val_accuracy: 0.8690
Epoch 6/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3752 - accuracy: 0.8675 - val_loss: 0.3718 - val_accuracy: 0.8724
Epoch 7/30
1719/1719 [==============================] - 7s 4ms/step - loss: 0.3631 - accuracy: 0.8716 - val_loss: 0.3616 - val_accuracy: 0.8736
Epoch 8/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3514 - accuracy: 0.8747 - val_loss: 0.3853 - val_accuracy: 0.8608
Epoch 9/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3412 - accuracy: 0.8793 - val_loss: 0.3573 - val_accuracy: 0.8718
Epoch 10/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3317 - accuracy: 0.8821 - val_loss: 0.3420 - val_accuracy: 0.8786
Epoch 11/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3238 - accuracy: 0.8839 - val_loss: 0.3450 - val_accuracy: 0.8770
Epoch 12/30
1719/1719 [==============================] - 6s 3ms/step - loss: 0.3147 - accuracy: 0.8865 - val_loss: 0.3306 - val_accuracy: 0.8832
Epoch 13/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3077 - accuracy: 0.8896 - val_loss: 0.3274 - val_accuracy: 0.8868
Epoch 14/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.3019 - accuracy: 0.8917 - val_loss: 0.3420 - val_accuracy: 0.8772
Epoch 15/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2943 - accuracy: 0.8940 - val_loss: 0.3222 - val_accuracy: 0.8842
Epoch 16/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2889 - accuracy: 0.8971 - val_loss: 0.3090 - val_accuracy: 0.8906
Epoch 17/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2835 - accuracy: 0.8979 - val_loss: 0.3546 - val_accuracy: 0.8736
Epoch 18/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2775 - accuracy: 0.9006 - val_loss: 0.3136 - val_accuracy: 0.8902
Epoch 19/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2726 - accuracy: 0.9024 - val_loss: 0.3110 - val_accuracy: 0.8904
Epoch 20/30
1719/1719 [==============================] - 8s 4ms/step - loss: 0.2671 - accuracy: 0.9036 - val_loss: 0.3271 - val_accuracy: 0.8818
Epoch 21/30
1719/1719 [==============================] - 6s 3ms/step - loss: 0.2621 - accuracy: 0.9056 - val_loss: 0.3066 - val_accuracy: 0.8926
Epoch 22/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2576 - accuracy: 0.9071 - val_loss: 0.2968 - val_accuracy: 0.8972
Epoch 23/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2533 - accuracy: 0.9086 - val_loss: 0.2997 - val_accuracy: 0.8936
Epoch 24/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2484 - accuracy: 0.9104 - val_loss: 0.3079 - val_accuracy: 0.8890
Epoch 25/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2442 - accuracy: 0.9127 - val_loss: 0.2977 - val_accuracy: 0.8948
Epoch 26/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2404 - accuracy: 0.9138 - val_loss: 0.3069 - val_accuracy: 0.8906
Epoch 27/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2360 - accuracy: 0.9155 - val_loss: 0.3040 - val_accuracy: 0.8940
Epoch 28/30
1719/1719 [==============================] - 6s 4ms/step - loss: 0.2327 - accuracy: 0.9166 - val_loss: 0.3003 - val_accuracy: 0.8934
Epoch 29/30
1719/1719 [==============================] - 6s 3ms/step - loss: 0.2284 - accuracy: 0.9181 - val_loss: 0.3050 - val_accuracy: 0.8908
Epoch 30/30
1719/1719 [==============================] - 6s 3ms/step - loss: 0.2248 - accuracy: 0.9203 - val_loss: 0.3055 - val_accuracy: 0.8934

모형을 만들고 훈련 시키는 것은 위 과정이 전부이다.
그러나, 초보자들이 흔히 하는 실수는 훈련 데이터와 검증 데이터의 크기가 맞지 않을 때 예외가 발생한다.

(8) 모델 평가

이제 모델을 평가합니다. 모델을 평가할 때는 보통 시각화를 통해서 확인합니다.
그리고, evaluate() 함수를 사용합니다.

import pandas as pd

pd.DataFrame(history.history).plot(figsize=(8, 5))
plt.grid(True)
plt.gca().set_ylim(0, 1)
save_fig("keras_learning_curves_plot")
plt.show()

그림 저장: keras_learning_curves_plot

png

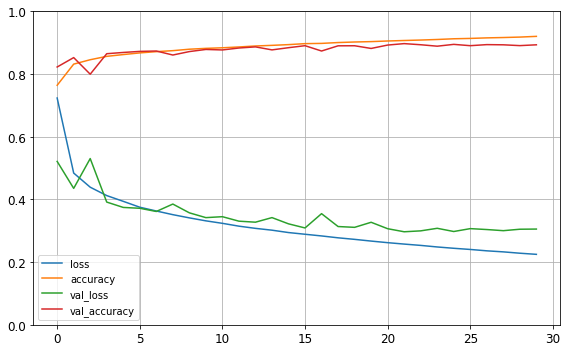
훈련 손실과 검증 손실은 감소하며, 또한 검증 곡선이 훈련 곡선과 가까우면, 과대적합하지 않았다는 증거가 된다.

model.evaluate(X_test, y_test)

313/313 [==============================] - 1s 3ms/step - loss: 0.3382 - accuracy: 0.8822





[0.3381877839565277, 0.8822000026702881]

(9) 모델 예측

이제 predict() 함수를 사용해 새로운 샘플에 대해 예측을 만든다.
새로운 샘플은 존재하지 않기 때문에 처음 3개의 샘플만 사용한다.

X_new = X_test[:3]
y_proba = model.predict(X_new)
print(y_proba.round(2))
y_pred = model.predict_classes(X_new)
print(y_pred)
print(np.array(class_names)[y_pred])

[[0.   0.   0.   0.   0.   0.01 0.   0.03 0.   0.96]
 [0.   0.   0.99 0.   0.01 0.   0.   0.   0.   0.  ]
 [0.   1.   0.   0.   0.   0.   0.   0.   0.   0.  ]]
[9 2 1]
['Ankle boot' 'Pullover' 'Trouser']

가장 높은 확률을 가진 클래스에만 관심이 있다면, predict_classes() 사용한다.

y_new = y_test[:3]
y_new

array([9, 2, 1], dtype=uint8)

실제 학습한 코드가 제대로 분류 되었는지 실제 이미지를 확인하는 차원에서의 코드를 다음과 같이 구현한다.

plt.figure(figsize=(7.2, 2.4))
for index, image in enumerate(X_new):
    plt.subplot(1, 3, index + 1)
    plt.imshow(image, cmap="binary", interpolation="nearest")
    plt.axis('off')
    plt.title(class_names[y_test[index]], fontsize=12)
plt.subplots_adjust(wspace=0.2, hspace=0.5)
save_fig('fashion_mnist_images_plot', tight_layout=False)
plt.show()

그림 저장: fashion_mnist_images_plot

png

IV. 금일 과제

교재를 참조하여 아래 예제를 연습한다.
- 함수형 API 모델 만들기
- 모형의 저장과 복원
- 훈련 과정에서의 Callback 사용하기

V. What’s Next

다음 시간에는 심층 신경망에 대해 학습하도록 한다.