Python 통계 - 비모수 통계
Page content
강의 홍보
- 취준생을 위한 강의를 제작하였습니다.
- 본 블로그를 통해서 강의를 수강하신 분은 게시글 제목과 링크를 수강하여 인프런 메시지를 통해 보내주시기를 바랍니다.
스타벅스 아이스 아메리카노를 선물로 보내드리겠습니다.
- [비전공자 대환영] 제로베이스도 쉽게 입문하는 파이썬 데이터 분석 - 캐글입문기
분포에 대한 가정을 만족 못할 시의 문제점
- 1종 오류의 값이 커지거나, 분석 결과 자체에 대한 신뢰성이 떨어짐
- 모수 통계 분석 적용 못할 시, 비모수 통계 분석 활용
(1) 언제 적용할까?
- 분포 가정 불만족 (예: 정규분포 아님)
- 분석기법의 전제조건 불만족 (예: 다중공선성)
- 표본 수 불만족 (예: 설문조사 20개)
- 데이터 척도 단순화 (예: 명목 또는 서열 척도로만 측정)
(2) 비모수 통계분석 유형
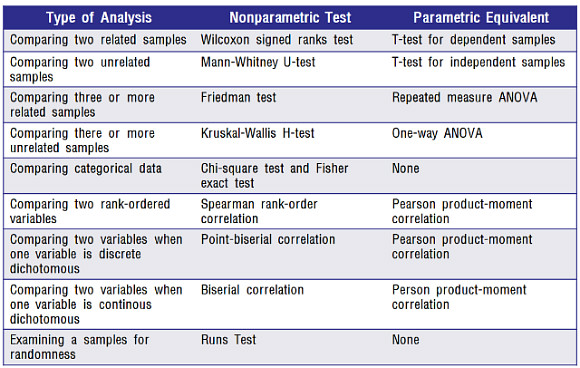
- 비모수 통계분석의 유형은 아래와 같다. (p. 357)
통계분석 실습 - 적합도 검정
(1) 적합도 검정: RUN 검정
- 가정된 확률이 정해져 있는 경우, 예) 제품의 A등급(6), B등급(3), C등급(1)
- 적합도 검정 예시
- 키워드: 측정도수 & 기대도수, RUN 검정
- 비모수 통계는 반대로, 표본의 배열이 무작위로 구성되어 있는지 검정
- (교재, p. 357)
- 마케팅 행사가 공정하게 이루어졌는지 RUN 검정 실시
- 가설검정
- 귀무가설: 멤버십 소지 고객과 비소지 고객의 방문은 무작위로 이루어짐
- 연구가설: 멤버십 소지 고객과 비소지 고객의 방문은 무작위로 이루어지지 않음
from statsmodels.sandbox.stats.runs import Runs
import numpy as np
x = [1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,0,0,0,0,0]
x = np.array(x)
Runs(x).runs_test()
(-1.8277470669267506, 0.06758752074917526)
- z값의 공식은 (RUN의 개수 - RUN의 평균) + 0.5 / RUN의 표준편차 (p.358) 참조
- 평균 및 표준편차를 구하는 방식은 모수의 방식과 다르다 (주의)
- -1.8은 z값을 의미하고, p 값은 0.067로 도출됨으로 유의수준 0.1 수준에서 유의하다.
- 즉, 연구가설을 채택하는데, 이 말의 함의는 공정하게 이루어지지 않았음을 의미
(2) Kolmogorov-Smirnov 검정
-
표본의 분포가 가정한 분포와 적합한지 검정 $$D_{n} = max|F_{n}(x) - F_{0}(x)$$
-
$D_{n}$이 임계치보다 작으면 귀무가설 채택하며, 이는 곧 $F_{n}(x)$와 $F_{n}(x)$는 차이가 나지 않기 때문에 가정한 분포와 표본의 분포가 적합
-
반대로 $D_{n}$이 임계치보다 크면 연구가설 채택하며, 이는 곧 $F_{n}(x)$와 $F_{n}(x)$는 차이가 있기 때문에 가정한 분포와 표본의 분포가 적합하지 않다고 해석.
-
정규 근사의 식은 다음과 같음 $$Z = \sqrt{n}D$$
-
여행 패키지 상품에 대한 만족도 조사 위해 40명의 참가 고객들을 대상으로 설문을 응답 받음
- 다양한 마케팅 가설검증 전, 정규분포성을 띄는지
Kolmogorov-Smirnov검정 수행
- 다양한 마케팅 가설검증 전, 정규분포성을 띄는지
-
가설검정
- 귀무가설: 고객들의 고객만족도점수는 정규분포를 따른다.
- 연구가설: 고객들의 고객만족도점수는 정규분포를 따르지 않는다.
from statsmodels.stats.diagnostic import kstest_normal
import numpy as np
x = [88, 75, 79, 84, 68, 51, 70, 75, 88, 90,
92, 88, 63, 72, 94, 80, 78, 98, 81, 67,
85, 87, 79, 81, 85, 48, 79, 86, 53, 100,
87, 80, 80, 32, 60, 75, 62, 82, 40, 57]
x = np.array(x)
kstest_normal(x, dist='norm')
(0.16508249090030575, 0.007697422359967707)
- kstest_normal(data, dist)이다.
dist는 검정할 분포로서 norm(정규분포), exp(지수분포) 두 가지를 설정할 수 있음 - 검정통계량 0.165, p값은 0.007
- 유의수준보다 작게 나와 연구가설을 따르며, 위 데이터는 정규분포를 따르지 않는다고 볼 수 있음
통계분석 실습 - 동질성 검정
- Wilcoxon 부호-순위 검정, Mann Whitney U 검정, Friedman 검정, 그리고 Kruskal-Wallis H 검정
(1) Wilcoxon 부호-순위 검정
- 쌍체 표본 t-검정에서 표본의 수가 30개 미만일 경우에 활용한다.
- Wilcoxon 부호-순위 검정의 절차는 교재 364 페이지를 참고한다.
- 가설 검증
- 배경: 기존의 물류 알고리즘보다 개선되었다고 알려진 새로운 물류 경로 최적화 알고리즘을 도입해 상품의 배송시간을 단축하고자 한다.
- 귀무가설: 기존 물류 알고리즘과 신규 알고리즘간을 통한 평균 배송시간은 차이가 없다.
- 대립가설: 기존 물류 알고리즘과 신규 알고리즘간을 통한 평균 배송시간은 차이가 있다.
from scipy.stats import wilcoxon
x = [10, 30, 9, 21, 35, 12, 17]
y = [8, 27, 16, 25, 30, 13, 11]
wilcoxon(x, y)
WilcoxonResult(statistic=12.0, pvalue=0.7353166906373405)
- 검정 통계량이 12.0, p-value은 0.735로 출력되었는데, 이는 귀무가설을 기각하지 못하므로 신규 알고리즘을 도입할 필요가 없다.
(2) Mann-Whitney U 검정
- 두 개의 독립된 집단간의 특정 값의 평균 비교
- 이 때, 두 개의 독립된 집단이 정규분포를 따르지 않을 때 사용한다.
- 연구 배경: V 반도체 회사는 공장 A와 공장 B 2개의 공장에서 반도체를 생산하고 있다. 이 때, 2개 공장의 생산 효율성에 차이가 있는지를 Mann-Whitney U 검정을 통해 살펴본다.
- 가설검정
- 귀무가설 = 공장 A와 공장 B의 생산효율성은 동일하다
- 연구가설 = 공장 A와 공장 B의 생산효율성은 다르다.
import pandas as pd
from scipy.stats import mannwhitneyu
x = [12, 11, 13, 14, 15]
y = [16, 15, 17, 19, 20]
print(mannwhitneyu(x, y))
# 생산량 평균 순위 출력
xy = pd.DataFrame(x+y)
xy['생산량 순위'] = xy.rank(ascending=False)
xy['공장이름'] = ["A", "A", "A", "A", "A", "B", "B", "B", "B", "B"]
print(xy.groupby('공장이름').mean())
MannwhitneyuResult(statistic=0.5, pvalue=0.007985348176890053)
0 생산량 순위
공장이름
A 13.0 7.9
B 17.4 3.1
- 검정통계량이
0.5그리고 유의확률은 0.0079이므로 귀무가설을 기각한다. - 즉, A와 B의 공장 생산의 효율성은 다르며, A의 효율성이 떨어지는 것을 볼 수 있다.
(3) Kruskal-Wallis H 검정
- 3개 이상의 독립 표본집단간의 본포가 동일한지 비교하는 검정 방법
- 일원분산분석과 유사한 목적을 지님
- 연구배경: Q제철기업은 철근을 생산하는데 있어 3개의 공장을 운영하고 있다. 생산량이 가장 낮은 공장을 찾아 공장 설비 등을 보강시켜 생산량을 높일 계획이다.
- 가설검증
- 귀무가설: 3개의 공장의 철근 생산량은 모두 동일하다.
- 연구가설: 3개의 공장의 철근 생산량은 모두 동일하지는 않다.
import pandas as pd
from scipy.stats import kruskal
a = [35, 41, 45, 42, 33, 36, 47, 45, 31, 32, 40, 44]
b = [40, 38, 44, 48, 45, 46, 42, 39, 40, 41, 38, 47]
c = [30, 34, 38, 39, 40, 41, 38, 37, 40, 41, 39, 38]
# Kruskal-Wallis H 검정 분석
print(kruskal(a, b, c))
# 생산량 평균 순위 출력
data = pd.DataFrame(a+b+c)
data["생산량순위"] = data.rank(ascending=False)
data["공장이름"] = ''
data["공장이름"][0:12] = 1
data["공장이름"][12:24] = 2
data["공장이름"][24:36] = 3
print(data.groupby("공장이름").mean())
KruskalResult(statistic=6.047476974964328, pvalue=0.04861911622342764)
0 생산량순위
공장이름
1 39.250000 19.0
2 42.333333 13.0
3 37.916667 23.5
- 통계량은
6.047476974964328,p-value는0.04이며, 이는 귀무가설을 기각하고, 연구가설을 채택한다.- 즉, 3개의 철근 생산량을 모두 동일하지 않으며, 그 중에서도 공장 3의 평균 생산량 순위가 가장 낮음을 알 수 있다.
(4) Friedman 검정
- 실험유형과 집단유형으로 구분된 여러 집단들의 서열정보를 사용하여 실험효과를 검증하는 방법
- 실험유형에 대해 다수의 쌍체표본 집단을 할당하고 서열을 이용하여 차이를 검정한다.
- A쇼핑 본사에서는 멤버십 VIP 고객들을 대상으로 새로운 혜택을 제공하고자 한다.
- 샘플증정, 포인트 추가, 무료배송, 할인쿠폰 등 4가지 혜택에 대한 5개 지역별 고객들에 대한 사전 선호도 조사를 실시하였다.
- 가설검정
- 귀무가설 = 혜택별 고객의 선호도 평가에 차이는 없다.
- 연구가설 = 혜택별 고객의 선호도 평가에 차이는 있다.
from scipy.stats import friedmanchisquare
a = [1,2,1,1,2]
b = [3,3,3,2,1]
c = [2,4,4,4,3]
d = [4,1,2,3,4]
friedmanchisquare(a, b, c, d)
FriedmanchisquareResult(statistic=6.359999999999999, pvalue=0.09535032301698126)
- 코드 실행 결과 검정통계량 6.360, p값은 0.095로 출력된다.
- 유의수준 0.05보다 크므로 귀무가설을 기각할 수 없다.
- 즉, VIP고객들에게는 신규 혜택에 대한 큰 메리트는 없기 때문에, 새로운 혜택을 고려해보는 것이 필요할 수도 있음을 의미한다.
통계분석 실습 - 상관성 검정
- 서열 정보를 이용한 상관성 검정에는 스피어만 서열상관분석과 Kendall 서열 상관분석을 사용할 수 있다.
- 피어슨, 스피어만, 정준상관분석에 대한 설명은 교재 145페이지를 참고한다.
- 피어슨 및 스피어만 상관분석은 7장에서 이미 다루었기 때문에, Kendall 서열상관분석만 다루도록 한다.
(1) Kendall 서열상관 계수 분석
- 분석 배경: H 홈쇼핑에서 주력 판매 품목이었던 의류/패션 상품의 매출이 급락하여 시급한 대책마련이 필요하게 되었다. 최근 판매된 5개 의류 브랜드의 가격과 판매량을 바탕으로 Kendall의 서열상관 계수를 구한다.
- 연구가설:
- 귀무가설 = H홈쇼핑의 의류브랜드 가격 서열과 판매량 서열은 연관성이 없다.
- 연구가설 = H홈쇼핑의 의류브랜드 가격 서열과 판매량 서열은 연관성이 있다.
from scipy.stats import kendalltau
x = [5, 2, 4, 1, 3]
y = [4, 1, 3, 2, 5]
kendalltau(x, y)
KendalltauResult(correlation=0.39999999999999997, pvalue=0.48333333333333334)
- 상관계수는 0.4, P값은 0.483, 즉 귀무가설을 기각하지 못한다. 따라서, 홈쇼핑의 최근 의류 판매 브랜드의 판매 가격 서열과 판매량 서열은 서로 연관성이 없다고 해석해야 한다.
- 즉, 판매량 저조의 문제점을 다른 곳에서 찾아야 한다는 뜻이다.
Reference
김형수. (2020). Step by Step 파이썬 비즈니스 통계분석. 서울: 프레딕스.

