결정 트리 학습 이론

Decision Tree, Python
Page content

개요

결정 트리의 예

  • 결정 트리는 여러가지 연속된 질문을 학습하여 분류하는 것이 원칙이다.
  • 다음의 간단한 예를 들어본다.

  • 결정 트리는 크게 3가지로 구성이 되어 있다.
    • 트리 내부 노드, 리프 노드, 그리고 가지로 구성이 되어 있다.
    • 어떻게 질문을 하느냐에 따라서 분류가 결정된다.
  • 결정 트리는 숫자에도 적용할 수 있다.
    • 예) 키가 160cm보다 큰가요?

결정 트리의 주요 원리

  • 결정 트리는 트리의 루트(Root)에서 시작하여, 정보 이득(Information Gain, IG)가 최대가 되는 특성으로 데이터를 나눔
  • 반복 과정(분류할 수 있는 연속적인 질문)을 통해 계속적으로 분류함
    • 전문 용어로는 Until the leaves are pure.
  • 결정 트리에서 가장 중요한 것은 정보 이득 최대화임(Maximizing Information Gain)

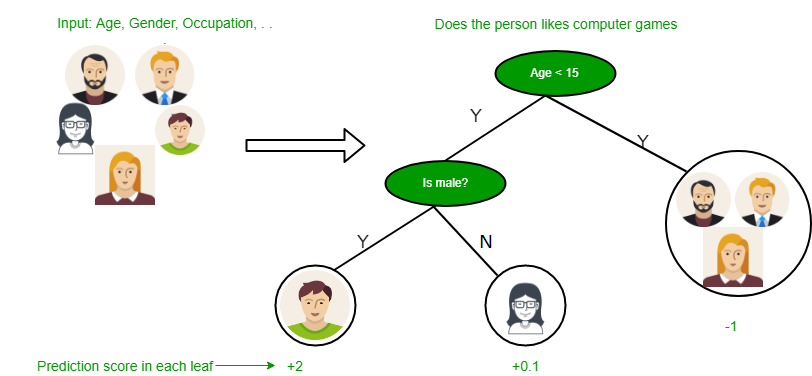
  • 이진 결정 트리에 널리 사용되는 세 개의 불순도 지표 또는 분할 조건은 다음과 같다.
    • 지니 불순도(Gini Impurity, $I_{G}$)
    • 엔트로피(Entropy, $I_{H}$)
    • 분류 오차(Classification Error, $I_{E}$)

주요 이론 1. 정보 이득의 정의

  • 정보 이득 수식은 다음과 같이 정의 할 수 있다. $$ IG(D_{p}, f) = I(D_{p}) - \sum_{j=1}^{m}\frac{N_{j}}{N_{p}}I(D_{j}) $$

  • 여기서 $f$는 분할에 사용할 특성이다.

  • $D_{p}$와 $D_{j}$는 부모와 $j$번째 자식 노드의 데이터셋을 의미한다.

  • $I$는 불순도(Inpurity) 지표를 말한다.

  • $N_{p}$는 부모 노드에 있는 전체 샘플 개수를 말한다.

  • $N_{j}$는 $j$번째 자식 노드에 있는 샘플 갯수를 말한다.

  • 부모 노드의 불순도와 자식 노드의 불순도 합의 차이이다.

    • 자식 노드의 불순도가 낮으면 낮을수록 정보 이득이 커진다. (the lower the impurity of the child nodes, the larger the information gain.)

  • 대부분의 라이브러리는 이진 결정 트리 사용(Binary Decision Trees)

    • 각 부모 노드는 두개의 자식 노드를 가진다. ($D_{left}$, $D_{right}$)

$$ IG(D_{p}, f) = I(D_{p}) - \frac{N_{left}}{N_{p}}I(D_{left}) - \frac{N_{right}}{N_{p}}I(D_{right}) $$

엔트로피의 정의

  • 샘플이 있는 모든 클래스$(p(i|t)\neq 0)$에 대한 정의는 다음과 같다. $$ I_{H}(t) = - \sum_{i=1}^{c}p(i|t)\log_{2}p(i|t) $$
  • 여기에서 $p(i|t)$는 특정 노드 $t$에 속한 샘플 비율
  • 한 노드의 모든 샘플이 같은 클래스면 엔트로피는 0임
  • 클래스 분포가 균등하면 엔트로피는 최대가 됨.
    • $p(i=1|t)=1$ 또는 $p(i=0)|t)=0$이면 엔트로피는 0임
    • 클래스가 $p(i=1|t)=0.5$와 $p(i=0)|t)=0.5$처럼 균등하게 분포가 되어 있으면 엔트로피는 1임
    • $\log_{2}(0.5)$는 -1이므로 두 노드가 균등하게 분포가 되어 있으면 아래와 같은 식이 도출됨.
      • $I_{H}(t)=-(0.5\times(-1) + 0.5\times(-1)) = 1$
    • 엔트로피 조건은 트리 내부의 상호 정보를 최대화하려고 시도 (the entropy criterion attempts to maximize the mutual information in the tree.)

지니불순도(Gini Information)

  • 잘못 분류될 확률을 최소화하기 위한 기준으로 이해
  • 지니 불순도는 만약의 클래스들이 완벽하게 섞여 있으면 최대치가 됨.
    • Binary Class Setting(C=2) $$ I_{G}(t) = 1 - \sum_{i=1}^{c}0.5^{2} = 0.5 $$

분류 오차(Classification Error)

  • 분류 오차의 정의는 다음과 같다. $$ I_{E} = 1-max { (p(i|t)) } $$

References

Raschka, S., & Mirjalili, V. (2017). Python Machine Learning - (2nd ed.). Packt Publishing.