입문자를 위한 머신러닝 분류 튜토리얼 - Decision Tree
Page content
개요
- 사이킷런(
scikit-learn)은 파이썬 머신러닝 라이브러리이다. - 파이썬에서 나오는 최신 알고리즘들도 이제는 사이킷런에 통합하는 형태로 취하고 있다.
- 구글 코랩은 기본적으로 사이킷런까지 설치가 완료되기에 별도의 설치가 필요없는 장점이 있다.
- Note: 본 포스트는 머신러닝 자체를 처음 접하는 분들을 위한 것이기 때문에, 어느정도 경험이 있으신 분들은 필자의 다른 포스트를 읽어주시기를 바랍니다.
패키지 불러오기
- 패키지는 시간에 지남에 따라 계속 업그레이드가 되기 때문에 꼭 버전 체크를 하는 것을 권장한다.
- 필자가 글을 남겼을 때는 2020년 8월 16일에 작성했음을 기억하자.
import sklearn
print(sklearn.__version__)
0.22.2.post1
머신러닝 워크플로우
- 가장 간단한 데이터인
iris데이터의 종 분류를 진행하도록 한다. - 사실, 이 예제는 매우 간단하기 때문에, 전체적인 프로세스를 익히는 관점에서 확인하기를 바란다.
(1) 지도학습의 정의
- 지도학습(Supervised Learning)의 가장 큰 특징 중의 하나는 위와 같이 분류 결정값이 사전에 정의가 되어야 한다.
- 만약, 사전에 분류가 된 것이 없다면 어떻게 할 수 있을까? 당연한 말이지만, 머신러닝 수행하기 전 데이터 수집이 필수가 된다.
- 위 꽃을 분류하는 것 같이, 명확한 정답이 주어진 데이터를 먼저 학습 한 뒤, 미지의 정답을 예측하는 것을 지도학습이라 부른다.

(2) Iris(붓꽃)이란
-
IRIS 붓꽃의 종류는 아래와 같이 3가지로 구성되어 있다.
Versicolor,Setosa,Virginica
-
위 이미지에서 보는 것처럼, 종에 따라 잎의 크기가 다른 것을 확인할 수 있다. 이제 예제 데이터를 불러오는 것부터 시작해보자.
(3) 데이터 불러오기
- 기본적으로
sklearn패키지내에는 내장 데이터가 있다.- sklearn 패키지내의 데이터셋은 조금 다르다 (참고: load_iris¶)
from sklearn.datasets import load_iris # 패키지 불러오기
# Bunch 형태의 데이터셋으로 구성되어 있음
iris = load_iris()
# 독립변수로만 구성된 데이터를 NumPy 형태로 가지고 있음
iris_data = iris.data
# iris.target은 붓꽃 데이터 세트에서 레이블을 NumPy로 가지고 있다.
iris_label = iris.target
print('iris target값:', iris_label[[0, 50, 100]])
print('iris target명:', iris.target_names)
iris target값: [0 1 2]
iris target명: ['setosa' 'versicolor' 'virginica']
- 위와 같이 데이터 세트를 확인하였다면 이제 하나의 데이터프레임으로 만들어봅니다.
import pandas as pd
iris_df = pd.DataFrame(data = iris_data, columns = iris.feature_names)
iris_df['label'] = iris.target
print(iris_df.head(3).to_markdown())
| | sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | label |
|---:|--------------------:|-------------------:|--------------------:|-------------------:|--------:|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
- 이 때, column명을 모두 바꾼다.
- sepal_length, sepal_width, petal_length, petal_width, species
- 또한, 시각화를 위해 species의 0, 1, 2를 [‘setosa’ ‘versicolor’ ‘virginica’] 형태로 바꾼다.
- 이 때,
map()함수를 사용한다.
- 이 때,
temp_data = iris_df.copy()
replace_fct = {0: 'setosa', 1: 'versicolor', 2: "virginica"}
temp_data.columns = ["sepal_length", "sepal_width", "petal_length", "petal_width", "species"]
temp_data['species'] = temp_data['species'].map(replace_fct)
temp_data.head(3).to_markdown()
'| | sepal_length | sepal_width | petal_length | petal_width | species |\n|---:|---------------:|--------------:|---------------:|--------------:|:----------|\n| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |\n| 1 | 4.9 | 3 | 1.4 | 0.2 | setosa |\n| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |'
(4) 데이터 시각화
- 데이터 시각화는 매우 중요하다.
- 시각화를 통해서 데이터의 패턴을 찾을 수 있기 때문이다.
- 여기에서는 우선 각 수치형 데이터에 관한 산점도를 작성한다.
- 또한 수치형 산점도를 종별로 그룹화하는 시각화를 작성해본다.
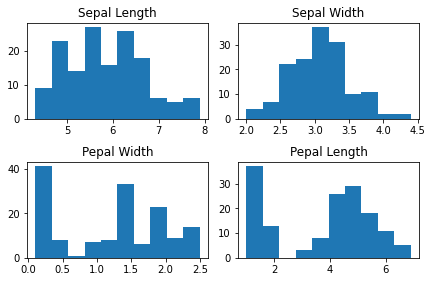
import matplotlib.pyplot as plt
n_bins = 10
fig, axs = plt.subplots(2, 2) # 그래프를 그리기 위해 일종의 레이아웃을 작성한다.
axs[0, 0].hist(temp_data['sepal_length'], bins = n_bins);
axs[0, 0].set_title('Sepal Length');
axs[0, 1].hist(temp_data['sepal_width'], bins = n_bins);
axs[0, 1].set_title('Sepal Width');
axs[1, 0].hist(temp_data['petal_width'], bins = n_bins);
axs[1, 0].set_title('Pepal Width');
axs[1, 1].hist(temp_data['petal_length'], bins = n_bins);
axs[1, 1].set_title('Pepal Length');
fig.tight_layout(pad=1.0);
- 이번에는 산점도를 작성한다.
import seaborn as sns
sns.pairplot(temp_data, hue="species", height = 2, palette = 'colorblind');
/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.
import pandas.util.testing as tm
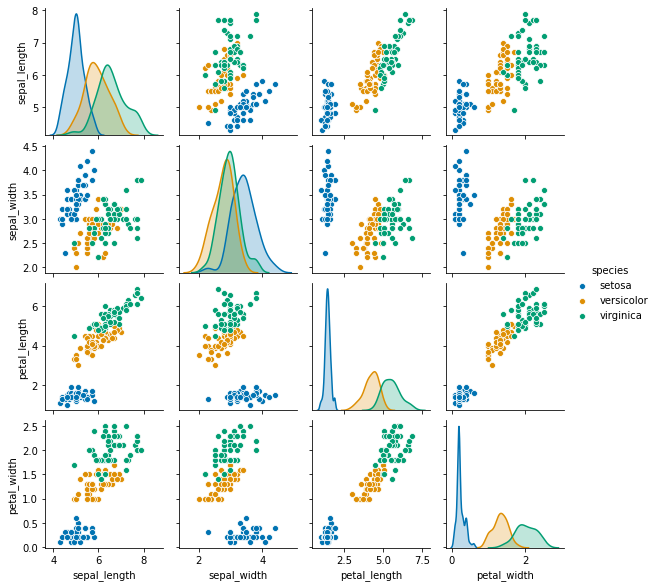
- 위 그래프에서 볼 수 있는 것처럼, 각 수치형 데이터의 크기에 따라 종의 구분이 되는 것을 볼 수 있다.
- 그러나, 몇몇 부분에서는 완벽하게 구분이 되지 않기 때문에, 다양한 변수의 조합을 통해 구분하는 작업이 필요하다.
(5) 데이터셋 분리
- 이제 학습용 데이터와 테스트용 데이터를 분리해보도록 한다.
- 학습 데이터로 모형을 만들었으면 실제 이 모형이 어느정도의 성능을 가지는지 평가할 필요가 있다.
- 사이킷런은
train_test_split()API를 제공한다. - 소스코드를 통해서 한번 확인해보자.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris_data, # 독립변수
iris_label, # 종속변수
test_size = 0.2,
random_state = 1)
- 위 코드에서
test_size는 훈련데이터와 테스트데이터로 나누는 비율이다. - 이제 본격적으로 분류기를 만들어본다.
(6) 머신러닝 모형 학습
- 이제 머신러닝 모형을 생성 합니다.
- 트리모형의 장점
- 데이터 전처리가 필요하지 않다.
- 특성의 스케일 또는 평균을 원점에 맞추는 작업 불필요하다.
- 모형의 해석은 시각화 이후 진행한다.
from sklearn.tree import DecisionTreeClassifier
# 객체 생성
dt_clf = DecisionTreeClassifier(random_state=11, max_depth=2)
# 학습 수행
dt_clf.fit(X_train, y_train)
DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
max_depth=2, max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort='deprecated',
random_state=11, splitter='best')
- 이제 의사 결정 트리 기반의
DecisionTreeClassifier객체는 학습 데이터를 기반으로 학습이 완료가 되었다. max_depth를2로 세팅한다.
(7) 모형 테스트
- 이제 모형을 예측해보자
from sklearn.metrics import accuracy_score
pred = dt_clf.predict(X_test)
print('The accuracy of the Decision Tree is: {:.3f}'.format(accuracy_score(pred,y_test)))
The accuracy of the Decision Tree is: 0.967
- 최종적인 정확도는
0.967인 것으로 확인되었다.
(8) 모형 결과 시각화 (Reporting)
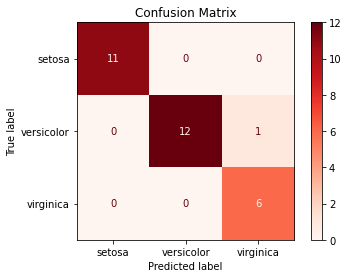
- 모형 결과에 대해 혼동행렬로 시각화 본다.
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import plot_confusion_matrix
labels = ['setosa', 'versicolor', 'virginica']
disp = plot_confusion_matrix(dt_clf,
X_test, y_test,
display_labels=labels,
cmap=plt.cm.Reds,
normalize=None)
disp.ax_.set_title('Confusion Matrix');
- 적합한
Tree모형을 시각화를 해본다.
import matplotlib.pyplot as plt
explt_vars = ["sepal_length", "sepal_width", "petal_length", "petal_width"]
fct_val = {0: 'setosa', 1: 'versicolor', 2: "virginica"}
plt.figure(figsize = (10,8))
plot_tree(dt_clf, feature_names = explt_vars, class_names = fct_val, filled = True);
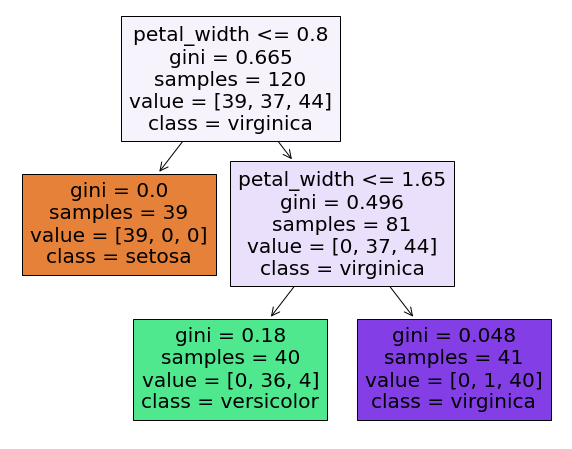
- 먼저 뿌리 노드(
root node)에서 시작한다.- 이 때, petal_width <= 0.8cm 보다 짧은지 확인한 후, 만약
True이면gini=0.0인 것으로 이동한다. - 이 경우 이 노드가
leaf node이므로 추가적인 검사를 하지 않고, 종 분류라고 예측 한다.
- 이 때, petal_width <= 0.8cm 보다 짧은지 확인한 후, 만약
False인 경우, 두번째로petal_width <= 1.65를 에서 만약True이면 gini0.18로 이동한 후 분류를 진행한다.- 만약
False인 경우에는 반대쪽으로 이동 후 최종적으로 분류한다.
- 만약
(9) 모형 해석 - 지니 불순도
-
지니 불순도의 개념
- 한 노드의 모든 샘플이 같은 클래스에 속해 있다면 이 노드를 순수(gini=0)이라고 함 $$G_{i} = 1 - \sum_{k=1}^{n}\left ( P_{i,k} \right )^{2}$$
-
위
gini=0.18나온 것을 확인하면 다음과 같다.
gini = 1 - (0/40)**2 - (36/40)**2 - (4/40)**2
print('The value of Gini is: {:.3f}'.format(gini))
The value of Gini is: 0.180
- 아래 코드는 핸즈온 머신러닝에서 발췌하였다.
from matplotlib.colors import ListedColormap
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import numpy as np
iris = load_iris()
X = iris.data[:, 2:] # 꽃잎 길이와 너비
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
if plot_training:
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris setosa")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris versicolor")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris virginica")
plt.axis(axes)
if iris:
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
if legend:
plt.legend(loc="lower right", fontsize=14)
plt.figure(figsize=(8, 4))
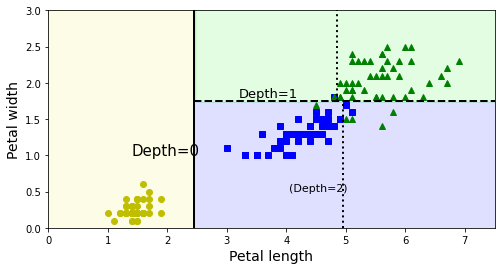
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
Text(4.05, 0.5, '(Depth=2)')
과적합에 대한 이해 및 해결 방안
-
과적합은 무엇일까?
- 과적합은 훈련데이터에 성능이 좋게 나타나지만, 실전에서는 정확도가 떨어지는 현상을 말한다.
- 내신 100점, 수능 50점의 학생
-
그렇다면 과적합을 해결하기 위해서 어떻게 해결해야 할까? 이 때 필요한 내용이
규제 매개변수라고 한다.
(1) 공식 홈페이지
- 자세한 내용은 Decition Trees에서 확인한다.
(2) 규제 매개변수
- 기본 개념: 훈련 데이터에 대한 과대적합을 피하기 위해 학습할 때, 결정 트리의 자유도를 제한한다.
- 기본값에서
None의 의미는 제한이 없음을 의미한다.- 즉, 과적합이 되기 싶다는 뜻이다.
- 규제 매개변수에 관한 대략적인 설명은 다음과 같다.
min_samples_split: 분할되기 위해 노드가 가져야 최소 샘플 수min_samples_leaf: 리프 노드가 가지고 있어야 할 최소 샘플 수min_weight_fraction_leaf: 가중치가 부여된 전체 샘플 수에서의 비율max_leaf_nodes: 리프 노드의 최대 수max_features: 각 노드에서 분할에 사용할 특성의 최대 수
min_으로 시작하는 것을 증가시키거나, 도는max_으로 시작하는 것을 감소시키면 모델에 규제가 커짐.pruning: 가지치기의 일종으로 순도를 높이는 것이 통계적으로 효과가 없다면리프 노드바로 위의 노드는 불필요하다. (이 때, 카이제곱 검정을 사용함).
소결
- 지금까지 배운 것을 종합해보면 다음과 같이 머신러닝 프로세스를 정리할 수 있다.
- 데이터 수집: 머신러닝 수행에 앞서 필수적인 데이터를 수집한다.
- 데이터 처리: 시각화를 위해 간단하게 데이터를 정리한다.
- 데이터 시각화: 주어진 데이터를 가지고 시각화를 작성한다.
- 데이터 세트 분리: 데이터를 학습 데이터와 테스트 데이터로 분리한다.
- 모델 학습: 학습 데이터를 기반으로
ML 알고리즘을 활용한다. - 예측 수행: 학습된 모델을 테스트 데이터로 확인 후 정확도를 확인한다.
- 평가: 이렇게 예측된 결과값과 테스트 데이터의 실제 결과값을 비교해 ML 모델 성능을 평가한다.

