머신러닝 지도학습 - 선형회귀
Page content
I. 개요
- 머신러닝으로서 회귀 모형에 대해 숙지한다.
- 회귀 모형의 기본적인 개념과 평가 지표에 대해 숙지한다.
II. 회귀 모형 개요
- 회귀(Regression)은 통계 이론 중 가장 기본이다.
- 회귀의 기원은 영국의 통계학자 갈톤(Galton)이 수행한 연구에서 유래한다.
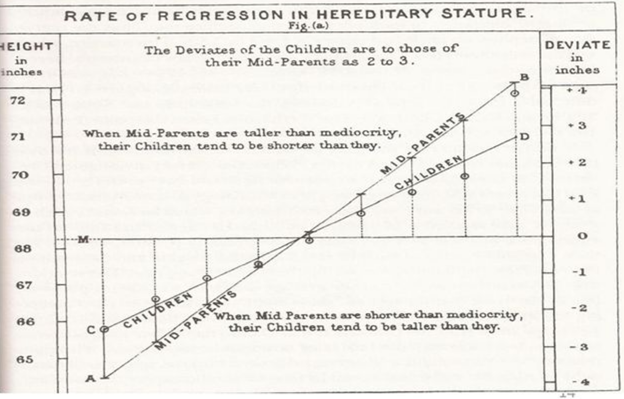
- 부모와 자식 간의 키의 상관관계를 분석하였는데, 키가 작은 가정과 키가 큰 가정을 살펴본 결과, 무한정 작아지지도 않고, 무한정 커지지 않아 일정한 평균으로 회귀하려는 자연적 법칙을 발견했다는 것이 기원이다.
(1) 회귀식의 개요
- 회귀는 1차 방정식이다.
- 지역, 방의 면적, 크기 등 여러 개의 독립변수에 따라 아파트 가격이라는 종속변수가 어떠한 관계를 나타내는지를 예측하고 모델링하는 것
- 즉, 수치를 예측할 때 사용한다.
$$ Y = W_{1}\times W_{1} + W_{2}\times W_{2} + W_{3}\times W_{3} + \cdot \cdot \cdot + W_{n}\times W_{n} $$
- 위 회귀식을 간단히 설명하면 다음과 같다.
- Y = 종속변수가 되며, 본 데이터에서는
MEDV에 해당된다. - $X_{1}$, $X_{2}$, $X_{3}$, $\cdot\cdot\cdot$, $X_{n}$은 지역, 방의 면적, 크기 등의 독립변수를 의미한다.
- $W_{1}$, $W_{2}$, $W_{3}$, $\cdot\cdot\cdot$, $W_{n}$은 회귀의 계수 등을 의미한다.
- 즉, 최적의 회귀 계수를 찾아가는 것이 회귀모형의 핵심이다.
- Y = 종속변수가 되며, 본 데이터에서는
- 간단한 예제를 통해 확인해보자.
import pandas as pd
from sklearn.datasets import load_boston
boston_raw = load_boston()
def sklearn_to_df(sklearn_dataset):
df = pd.DataFrame(sklearn_dataset.data, columns=sklearn_dataset.feature_names)
df['target'] = pd.Series(sklearn_dataset.target)
return df
df_boston = sklearn_to_df(boston_raw)
df_boston.shape
(506, 14)
df_boston
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | target | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 | 24.0 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 | 21.6 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 | 34.7 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 | 33.4 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 | 36.2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 0.06263 | 0.0 | 11.93 | 0.0 | 0.573 | 6.593 | 69.1 | 2.4786 | 1.0 | 273.0 | 21.0 | 391.99 | 9.67 | 22.4 |
| 502 | 0.04527 | 0.0 | 11.93 | 0.0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1.0 | 273.0 | 21.0 | 396.90 | 9.08 | 20.6 |
| 503 | 0.06076 | 0.0 | 11.93 | 0.0 | 0.573 | 6.976 | 91.0 | 2.1675 | 1.0 | 273.0 | 21.0 | 396.90 | 5.64 | 23.9 |
| 504 | 0.10959 | 0.0 | 11.93 | 0.0 | 0.573 | 6.794 | 89.3 | 2.3889 | 1.0 | 273.0 | 21.0 | 393.45 | 6.48 | 22.0 |
| 505 | 0.04741 | 0.0 | 11.93 | 0.0 | 0.573 | 6.030 | 80.8 | 2.5050 | 1.0 | 273.0 | 21.0 | 396.90 | 7.88 | 11.9 |
506 rows × 14 columns
- 각 데이터 변수에 대한 설명서를 제공하고 있다.
print(boston_raw.DESCR)
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
df_boston = df_boston.rename({"target": "MEDV"}, axis='columns')
- 간단하게 시각화를 진행한다.
import matplotlib.pyplot as plt
df_boston.plot(kind = "scatter", x = "LSTAT", y = "MEDV", alpha = 0.2, figsize = (10, 7))
*c* argument looks like a single numeric RGB or RGBA sequence, which should be avoided as value-mapping will have precedence in case its length matches with *x* & *y*. Please use the *color* keyword-argument or provide a 2-D array with a single row if you intend to specify the same RGB or RGBA value for all points.
<matplotlib.axes._subplots.AxesSubplot at 0x7ff882047978>
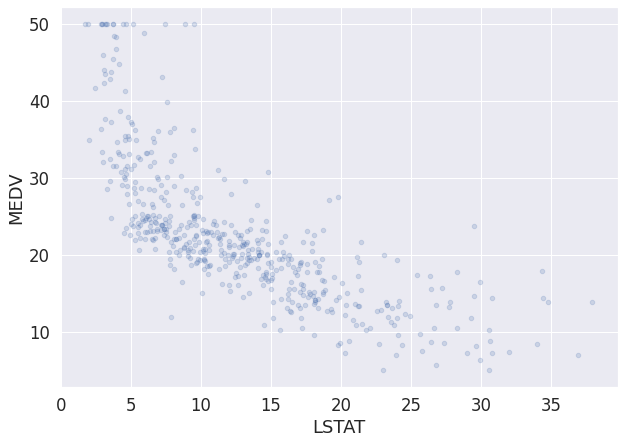
MEDV는 평균 값을 의미하며, 우리가 예측하려는 데이터와 같다.- 그런데, 데이터는 이렇게 변수 2개로 설명되는 일이 드물다.
- 위 데이터에서
cmap()을AGE변수를 추가하여 색상의 변동을 확인해보자.
df_boston.plot(kind = "scatter",
x = "LSTAT",
y = "MEDV",
alpha = 0.2,
label = 'Build Years',
s = df_boston['DIS'] * 50,
c = "AGE",
figsize = (10, 7),
cmap = plt.get_cmap('jet'), colorbar = True)
plt.legend()
<matplotlib.legend.Legend at 0x7ff881b3c4e0>
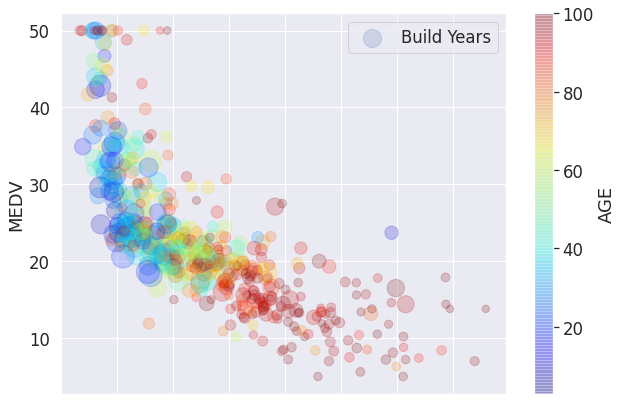
- 이제 위 그래프를 해석해보자.
(하위층) LSTAT이 증가할 수록MEDV은 작아지는 뚜렷한 경향성이 있다.- 인수
s는(직업센터) DIS거리를 나타낸다. 즉,five Boston employment centres와의 거리가 멀수록 상대적으로MEDV의 값이 커지는 것을 확인할 수 있었다. - 인수
c는 색상을 나타내는데,AGE는 1940년 이전에 건축된 주택의 비율을 의미하기 때문에, 색깔이 빨갛게 될 수록 건물이 오래되었다는 뜻이다.
- 종합하면,
MEDV가 높게 형성 되려면,LSTAT는 비율은 낮아야 하고,DIS와의 거리는 상대적으로 멀어야 하고,AGE는 가급적 낮아야 한다. - 위 결론의 내용은 어찌보면 당연한 얘기인 것처럼 보이지만, 시각적으로 증명하는 것이 쉬운 것은 아니다.
(2) 상관관계 분석
- 이러한 수치형 데이터를 다룰 때에는 보통 상관계수를 구하는데, 엄밀히 말하면 피어슨의 상관관계 계수(Pearson Product-Moment Correlation Coefficient)를 포함하고 있는 정방 행렬이다.
- 상관관계 계수의 범위는 -1~1 이다.
- r = 1이면, 두 특성이 완벽한 양의 상관관계를 가진다.
- r = 0이면, 두 특성에는 아무런 상관관계가 없다.
- r = -1이면, 두 특성에는 완벽한 음의 상관관계를 가진다.
- 이러한 상관계수를 뽑아내는 것은 seaborn 패키지를 활용하면 보다 쉽게 추출할 수 있다.
import numpy as np
import seaborn as sns
cols = ['LSTAT', 'DIS', 'AGE', 'RM', 'MEDV']
cm = np.corrcoef(df_boston[cols].values.T)
sns.set(font_scale = 1.5, rc={'figure.figsize':(11.7,8.27)})
hm = sns.heatmap(cm,
cbar = True,
annot = True,
square = True,
fmt = '.2f',
annot_kws = {'size':15},
yticklabels=cols,
xticklabels=cols)
plt.tight_layout()
plt.show()
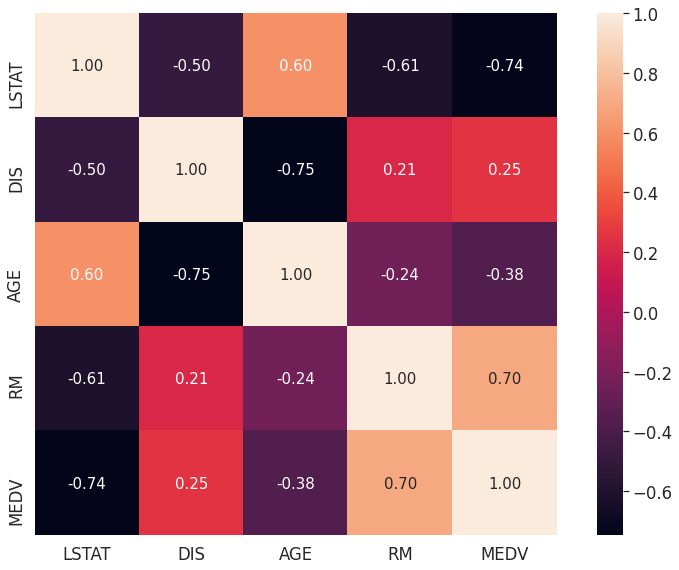
- 위 결과값이 무엇을 의미할까?
- 만약
MEDV를 제외한 4개의 변수 중 2개의 변수만 추출해야 한다면, 상관성이 높은LSTAT와RM의 변수를 선택하는 것이 좋다.
(3) Sklearn 회귀모형
LinearRegression클래스LinearRegression클래스는 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화해OLS(Ordinary Least Squares)추정 방식으로 구현한 클래스다.
- 입력 파라미터
- fit_intercept: intercept(절편) 값을 계산할 것인지 말지를 지정한다.
- normalize: 만약
True이면, 입력 데이터 세트를 정규화 한다.
- 속성
- coef_:
fit()메서드를 수행했을 때, 회귀 계수가 배열 형태로 저장하는 속성.
- coef_:
- 회귀 모형 시에는 다중공선성(
Multi-collinearity) 문제가 발생할 수 있다.
(4) 회귀 평가 지표
- 회귀 평가 지표는 일반적인 통계모형의 적합성 평가, 결정계수 등과 다르다.
- 머신러닝에서는 예측 지표가 우선이다.
- 실제 값과 회귀 예측값의 차이 값을 기반으로 한 지표가 중심이다.
- 회귀의 성능을 평가하는 지표는 다음과 같다.
- MAE(Mean Absolute Error): 실제 값과 예측값의 차이를 절대값으로 변환해 평균
- MSE(Mean Squared Error): 실제 값과 예측값의 차이를 제곱해 평균
- RMSE(Root Mean Squared Error):
MSE값은 오류의 제곱을 구하며, 실제 오류 평균보다 더 커지는 특성이 있어서MSE에Root를 쒸움 - $R^2$는 분산 기반으로 예측 성능을 평가 하고, 실제 값의 분산대비 예측값의 분산 비율을 지표로 하기 때문에, 1에 가까울수록 예측 정확도가 높다.
sklearn.metrics에는MAE,MSE, $R^2$가 있다,RMSE는 존재하지 않기 때문에MSE에Root를 씌워준다.
III. 실습
- 이제 훈련 및 테스트데이터를 만들어 예측 모형을 만들어본다.
(1) 데이터셋 분리
- 훈련 및 테스트 데이터를 분리한다.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 종속변수 및 독립변수 데이터 셋으로 분리
y_target = df_boston['MEDV']
X_data = df_boston.drop(['MEDV'], axis = 1, inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.3, random_state=1)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
((354, 13), (152, 13), (354,), (152,))
- 마지막 줄
shape를 습관적으로 해주는 것이 좋다.- 데이터의 행과 열이 일치하는지 확인한다.
(2) 회귀 모형 만들기
- 이제 모형을 만들어본다.
my_1st_lr = LinearRegression()
my_1st_lr.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
(3) 모형 예측
predict()함수를 활용해서X_test를 실행한다.
y_preds = my_1st_lr.predict(X_test)
y_preds[0:5]
array([32.3914647 , 27.94401279, 17.83762764, 21.66941388, 18.93639614])
0:5예측값에 대한 결과가 나온다.
(4) 회귀 계수
- 이번에는 절편 및 회귀 계수값을 구해본다.
- 이 회귀 계수는 각 변수에 대한 회귀 계수를 의미한다.
print("절편:", my_1st_lr.intercept_)
print('회귀 계수:', np.round(my_1st_lr.coef_, 1))
절편: 46.39649387182328
회귀 계수: [ -0.1 0.1 0.1 2.4 -21.5 2.8 0. -1.5 0.3 -0. -1. 0.
-0.6]
- 이번에는 회귀 계수가 큰 값 순으로 정렬한다. 이 때, 각 변수를 매칭 시켜서 중요 요인을 확인해본다.
coef_df = pd.Series(data=np.round(my_1st_lr.coef_, 1), index = X_data.columns)
coef_df.sort_values(ascending=False)
RM 2.8
CHAS 2.4
RAD 0.3
INDUS 0.1
ZN 0.1
B 0.0
TAX -0.0
AGE 0.0
CRIM -0.1
LSTAT -0.6
PTRATIO -1.0
DIS -1.5
NOX -21.5
dtype: float64
- 위 결과에서 보는 것처럼,
RM과NOX에서 회귀 계수 값이 가장 큰 것으로 나타났으며, 이는MEDV가격 형성에 매우 중요한 요소임을 확인할 수 있다.
(5) 모형 평가
- 회귀 모형에 대한 평가를 진행해본다.
RMSE는 없기 때문에, 새로 만들어야 한다.
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
r2_points = r2_score(y_test, y_preds)
print("RMSE:", rmse)
print("R^2:", r2_points)
RMSE: 4.4532374371981245
R^2: 0.7836295385076315
IV. 결론
- 지금까지 진행 한 것은 회귀모형에 대한 이해를 위한 것이며, 실제로는 위와 같이 선형 회귀 모형 1개만을 만들지 않는다.
- 특히 회귀 계수는 선형 회귀에만 나오는 개념이며, 나무모형, SVM은 또 다르다.
- 그럼 각각 일일이 다 공부하는 게 의미가 있는 것인가?
- 모든 통계 모형을 한꺼번에 다 공부하는 것은
지양한다.- 시간이 해결해준다. 그리고, 최신 논문을 늘 챙긴다.
- 이제 나무 모형으로 넘어간다. 현재 나오는 최신 알고리즘은 나무 모형에 기반하기 때문이다.
- 이 때, 우리가 기억해야 하는 것은 모형의 평가다.
- 예측에서 중요한 것은 예측값과 실제값의 오차를 줄이는 것. 이것만 기억하자.
