Seaborn intro - Correlation Heatmap
강의 홍보
- 취준생을 위한 강의를 제작하였습니다.
- 본 블로그를 통해서 강의를 수강하신 분은 게시글 제목과 링크를 수강하여 인프런 메시지를 통해 보내주시기를 바랍니다.
스타벅스 아이스 아메리카노를 선물로 보내드리겠습니다.
- [비전공자 대환영] 제로베이스도 쉽게 입문하는 파이썬 데이터 분석 - 캐글입문기
Seaborn 개요
Matplotlib 라이브러리가 Python에서 제공하는 기본적인 시각화 도구이지만, 기본객체는 리스트 형태를 따르기 때문에, 엑셀 데이터, 즉 데이터 프레임에 익숙한 사용자들에게는 조금 불친절한 것은 아쉬움이 있습니다. 실제, 입문자를 대상으로 강의를 할 때에도 Seaborn부터 알려드리는데, 그 이유는 Pandas를 활용한 데이터 가공 직후에 보다 쉽게 연동할 수 있도록 Seaborn이 개발되었기 때문입니다. 또한, Matplotlib에서는 회귀선과 같은 통계적 내용의 그래프도 보다 쉽게 구현할 수 있도록 제작되었습니다. 보다 정교한 시각적인 디자인을 추가 및 수정하려면, Matplotlib를 보다 더 잘 활용해야 합니다. 이는 마지막 본 포스트의 마지막 장에서 다루도록 합니다.
먼저, 간단한 예제를 통해서 익히도록 합니다.
라이브러리 불러오기
필요한 모듈을 불러옵니다.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
상관관계 히트맵
두 개 이상 변수들간의 상호 관련성을 판단하기 위해 상관관계 분석 및 시각화를 진행하고자 합니다. 상관관계 분석의 종류는 변수의 특성 및 표본의 개수에 따라 여러 갈래로 나눠지기도 합니다 (피어슨, 스피어만, 켄달, 점이연, 이연 상관계수 관련 표 작성). 본 장에서는 수치형 변수로 이루어진 두 변수간의 연관성 파악을 위해 시각화만 작성합니다.
보통 상관관계 분석을 한다고 하면, 피어슨 상관관계 분석(Pearson Correlation Analysis)를 의미합니다. 두 변수간의 선형적 관계의 강도를 r로 표현합니다.
A. 공분산과 상관계수
수치형 변수간의 상관관계를 나타내는 지표는 공분산(covariance)과 상관계수가 있는데, 공식은 아래와 같이 정의할 수 있습니다.
-
먼저 공분산 공식은 아래와 같다. $$(S_{xy}) = \frac{1}{n-1}\sum_{i=1}^{n}\left (x_{i}-\bar{x}\right)\times\left (y_{i}-\bar{y}\right)$$
-
상관계수 공식은 아래와 같다. $$r=\frac{S_{xy}}{S_{x}\times S_{y}}$$ 이때, $S_{xy}$는 xy의 표준편차를 의미하며, $S_{x}$는 x의 표준편차, $S_{y}$는 y의 표준편차를 의미한다.
먼저, 공분산의 의미는 결과 값이 양수일 경우에는 선형관계를, 음수일 경우에는 음의 선형관계가 존재함을 의미하는 방향성만 가지며, 선형관계의 강도 또는 정도를 표현하기 어렵기 때문에 상관관계 계수를 같이 표현합니다.
B. 상관계수 히트맵
상관관계 히트맵은 캐글에서도 빈번하게 자주 사용되어지는 시각화이기에 소개합니다. 시각화를 작성하는 순서는 원 데이터에서 수치형 위주의 데이터프레임 위주로만 추출한 후, corr() 함수를 사용하여 값을 구한후, heatmap()을 활용하면 됩니다.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
mpg = sns.load_dataset("mpg")
print(mpg.shape) # 398 행, 9개 열
num_mpg = mpg.select_dtypes(include = np.number)
print(num_mpg.shape) # 398 행, 7개 열
(398, 9)
(398, 7)
현재 모든 데이터가 문자열인 것을 확인할 수 있다.
num_mpg.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 398 entries, 0 to 397
Data columns (total 7 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 mpg 398 non-null float64
1 cylinders 398 non-null int64
2 displacement 398 non-null float64
3 horsepower 392 non-null float64
4 weight 398 non-null int64
5 acceleration 398 non-null float64
6 model_year 398 non-null int64
dtypes: float64(4), int64(3)
memory usage: 21.9 KB
먼저 각 데이터간의 상관계수를 구합니다.
num_mpg.corr()
| mpg | cylinders | displacement | horsepower | weight | acceleration | model_year | |
|---|---|---|---|---|---|---|---|
| mpg | 1.000000 | -0.775396 | -0.804203 | -0.778427 | -0.831741 | 0.420289 | 0.579267 |
| cylinders | -0.775396 | 1.000000 | 0.950721 | 0.842983 | 0.896017 | -0.505419 | -0.348746 |
| displacement | -0.804203 | 0.950721 | 1.000000 | 0.897257 | 0.932824 | -0.543684 | -0.370164 |
| horsepower | -0.778427 | 0.842983 | 0.897257 | 1.000000 | 0.864538 | -0.689196 | -0.416361 |
| weight | -0.831741 | 0.896017 | 0.932824 | 0.864538 | 1.000000 | -0.417457 | -0.306564 |
| acceleration | 0.420289 | -0.505419 | -0.543684 | -0.689196 | -0.417457 | 1.000000 | 0.288137 |
| model_year | 0.579267 | -0.348746 | -0.370164 | -0.416361 | -0.306564 | 0.288137 | 1.000000 |
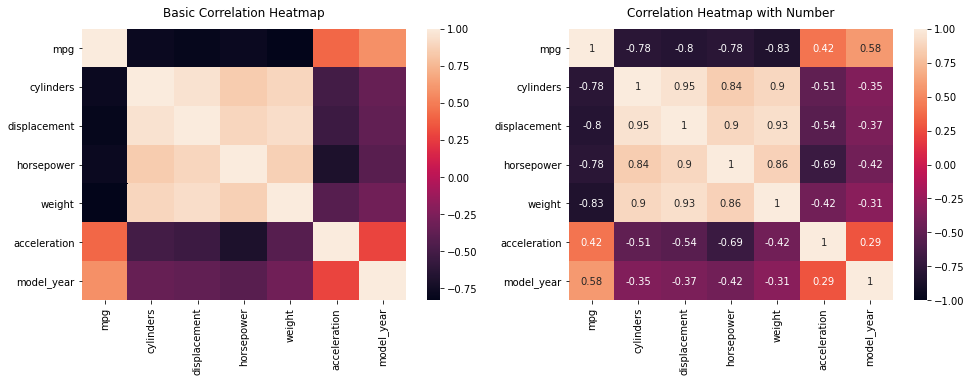
위 결과값에서 이제 heatmap()만 적용하면 시각화가 완성이 됩니다.
fig, ax = plt.subplots(nrows = 1, ncols = 2, figsize=(16, 5))
# 기본 그래프 [Basic Correlation Heatmap]
sns.heatmap(num_mpg.corr(), ax=ax[0])
ax[0].set_title('Basic Correlation Heatmap', pad = 12)
# 상관관계 수치 그래프 [Correlation Heatmap with Number]
sns.heatmap(num_mpg.corr(), vmin=-1, vmax=1, annot=True, ax=ax[1])
ax[1].set_title('Correlation Heatmap with Number', pad = 12)
plt.show()
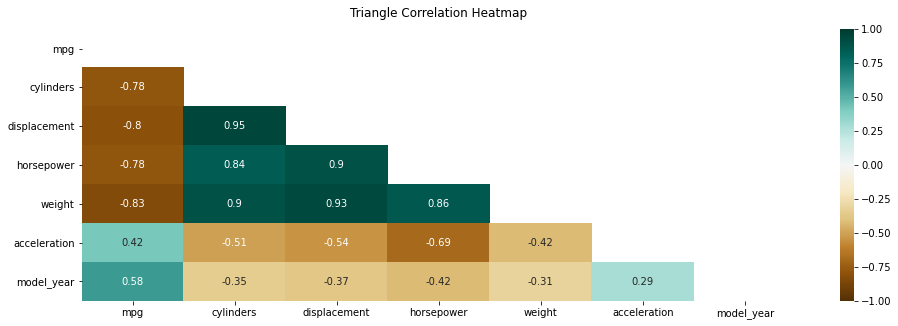
C. 상관계수 히트맵(직삼각형)
이번 코드 작성은 약간의 트릭(Trick)이 필요하며, heatmap() 안에 있는 mask 인수를 활용할 예정이다. mask는 각 값이 만약 True일 경우 Cell의 값이 보이지 않도록 해주는 기능이다.
이 때, np.triu() 함수를 활용하여 매트릭스의 우측상단을 모두 1로 만들어서 True값을 만든다. 이는 True값이 1이라는 프로그래밍 원리를 활용한 것이다.
print(int(True))
np.triu(np.ones_like(num_mpg.corr()))
1
array([[1., 1., 1., 1., 1., 1., 1.],
[0., 1., 1., 1., 1., 1., 1.],
[0., 0., 1., 1., 1., 1., 1.],
[0., 0., 0., 1., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 0., 1., 1.],
[0., 0., 0., 0., 0., 0., 1.]])
먼저 마스크 배열을 구한다.
# mask True/False 값 구하기
mask = np.triu(np.ones_like(num_mpg.corr(), dtype=np.bool))
print(mask)
[[ True True True True True True True]
[False True True True True True True]
[False False True True True True True]
[False False False True True True True]
[False False False False True True True]
[False False False False False True True]
[False False False False False False True]]
fig, ax = plt.subplots(figsize=(16, 5))
# 기본 그래프 [Basic Correlation Heatmap]
sns.heatmap(num_mpg.corr(),
mask=mask,
vmin=-1,
vmax = 1,
annot=True,
cmap="BrBG",
cbar = True)
ax.set_title('Triangle Correlation Heatmap', pad = 12)
plt.show()
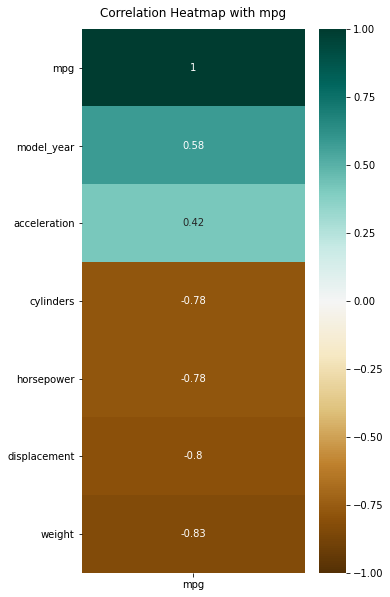
마지막 히트맵은 막대그래프와 같이 표시하되, 다만 색깔로 구분하는 것이다. 이 때 mpg를 반응변수로 판단하여, 반응변수에 대한 상관계수를 내림차순으로 정렬한다.
print(num_mpg.corr()[['mpg']].sort_values(by='mpg', ascending=False))
mpg
mpg 1.000000
model_year 0.579267
acceleration 0.420289
cylinders -0.775396
horsepower -0.778427
displacement -0.804203
weight -0.831741
이제 시각화를 구현하면 아래와 같다.
num_mpg_ylabels = num_mpg.corr()[['mpg']].sort_values(by='mpg', ascending=False).index.tolist()
num_mpg.corr()[['mpg']].sort_values(by='mpg', ascending=False).index
fig, ax = plt.subplots(figsize=(5, 10))
sns.heatmap(num_mpg.corr()[['mpg']].sort_values(by='mpg', ascending=False),
vmin = -1, vmax = 1, annot=True, cmap="BrBG")
ax.set_title('Correlation Heatmap with mpg', pad = 12)
ax.set_yticklabels(num_mpg_ylabels, rotation=0) # y축을 가로형으로 변환
plt.show()