Verifying Outlier Values
Page content
이상값의 정의
- 다소 주관적이며(Somewhat Subjective), 특정 분포의 중심경향성, 퍼진 정도와 형태에 따라 밀접한 관련이 있다.
- 평균에서 표준편차보다 몇 배 더 떨어져 있다거나, 즉, 정규분포를 이루고 있지 않을 때
- 왜도 또는 첨도가 발생할 때
- 균등분포(Uniform Distribution)는, 발생할 확률이 모두 같다.
- 만약, 확진자수가 최소 1부터 최대 10,000,000까지 균등하게 분포한다면, 어떤 값도 이상값으로 고려하지 않는다.
- 이상값을 파악하려면, 반드시, 각 변수의 분포를 먼저 이해해야 한다.
라이브러리 및 데이터 불러오기
- 실습을 위한 데이터를 불러온다.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
import scipy.stats as scistat
covidtotals = pd.read_csv("data/covidtotals.csv")
covidtotals.set_index("iso_code", inplace = True)
case_vars = ["location", "total_cases", "total_deaths", "total_cases_pm", "total_deaths_pm"]
demo_vars = ["population", "pop_density", "median_age", "gdp_per_capita", "hosp_beds"]
print(covidtotals.head())
lastdate location total_cases total_deaths total_cases_pm \
iso_code
AFG 2020-06-01 Afghanistan 15205 257 390.589
ALB 2020-06-01 Albania 1137 33 395.093
DZA 2020-06-01 Algeria 9394 653 214.225
AND 2020-06-01 Andorra 764 51 9888.048
AGO 2020-06-01 Angola 86 4 2.617
total_deaths_pm population pop_density median_age \
iso_code
AFG 6.602 38928341.0 54.422 18.6
ALB 11.467 2877800.0 104.871 38.0
DZA 14.891 43851043.0 17.348 29.1
AND 660.066 77265.0 163.755 NaN
AGO 0.122 32866268.0 23.890 16.8
gdp_per_capita hosp_beds
iso_code
AFG 1803.987 0.50
ALB 11803.431 2.89
DZA 13913.839 1.90
AND NaN NaN
AGO 5819.495 NaN
- describe() 함수를 통해 수치 데이터의 분포를 확인하도록 한다.
covid_case_df = covidtotals.loc[:, case_vars]
print(covid_case_df.describe())
total_cases total_deaths total_cases_pm total_deaths_pm
count 2.100000e+02 210.000000 210.000000 210.000000
mean 2.921614e+04 1770.714286 1355.357943 55.659129
std 1.363978e+05 8705.565857 2625.277497 144.785816
min 0.000000e+00 0.000000 0.000000 0.000000
25% 1.757500e+02 4.000000 92.541500 0.884750
50% 1.242500e+03 25.500000 280.928500 6.154000
75% 1.011700e+04 241.250000 1801.394750 31.777250
max 1.790191e+06 104383.000000 19771.348000 1237.551000
- 백분위수(quantile)로 데이터를 표시한다.
print(covid_case_df.quantile(np.arange(0.0, 1.1, 0.1)))
total_cases total_deaths total_cases_pm total_deaths_pm
0.0 0.0 0.0 0.0000 0.0000
0.1 22.9 0.0 17.9986 0.0000
0.2 105.2 2.0 56.2910 0.3752
0.3 302.0 6.7 115.4341 1.7183
0.4 762.0 12.0 213.9734 3.9566
0.5 1242.5 25.5 280.9285 6.1540
0.6 2514.6 54.6 543.9562 12.2452
0.7 6959.8 137.2 1071.2442 25.9459
0.8 16847.2 323.2 2206.2982 49.9658
0.9 46513.1 1616.9 3765.1363 138.9045
1.0 1790191.0 104383.0 19771.3480 1237.5510
- 왜도는 분포가 얼마나 대칭적인지를 나타냄
- 왜도와 첨도는 어떻게 대칭적인지를 설명하며, 분포의 꼬리가 각각 얼마나 두꺼운지 나타냄.
covid_case_df.skew(axis=0, numeric_only = True)
total_cases 10.804275
total_deaths 8.929816
total_cases_pm 4.396091
total_deaths_pm 4.674417
dtype: float64
covid_case_df.kurtosis(axis=0, numeric_only = True)
total_cases 134.979577
total_deaths 95.737841
total_cases_pm 25.242790
total_deaths_pm 27.238232
dtype: float64
- 정규성 검정을 테스트 한다.
- p값 0.05미만에서 95% 수준에서 정규분포의 귀무가설을 기각하고, 대립가설을 채택한다.
- 귀무가설: 표본의 모집단이 정규분포를 이루고 있다.
- 대립가설: 표본의 모집단이 정규분포를 이루고 있지 않다.
scistat.shapiro(covid_case_df['total_cases'])
ShapiroResult(statistic=0.19379639625549316, pvalue=3.753789128593843e-29)
scistat.shapiro(covid_case_df['total_deaths'])
ShapiroResult(statistic=0.19832086563110352, pvalue=4.3427896631016077e-29)
scistat.shapiro(covid_case_df['total_cases_pm'])
ShapiroResult(statistic=0.5220695734024048, pvalue=1.3972683006509067e-23)
scistat.shapiro(covid_case_df['total_deaths_pm'])
ShapiroResult(statistic=0.41877639293670654, pvalue=1.361060423265974e-25)
- 위 4개의 feature 모두 정규분포를 이루고 있지 않음을 확인할 수 있다.
- 이번에는 qqplot을 그린다.
sm.qqplot(covid_case_df[["total_cases"]].sort_values(["total_cases"]), line = "s")
plt.title("QQ Plot of Total Cases")
Text(0.5, 1.0, 'QQ Plot of Total Cases')
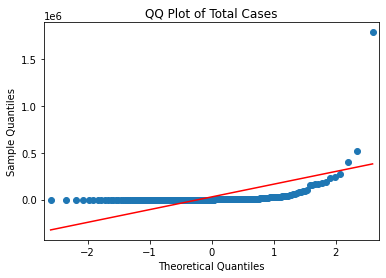
- 이번에는 정규분포를 이루는 샘플 데이터의 shapiro 검정 테스트와 qqplot을 그려본다.
random_normal_datapoints = pd.Series(np.random.normal(0, 0.1, 200))
print(scistat.shapiro(random_normal_datapoints))
ShapiroResult(statistic=0.9939591884613037, pvalue=0.5945821404457092)
sm.qqplot(random_normal_datapoints, line = "s")
plt.title("QQ Plot of Normal Datapoints")
Text(0.5, 1.0, 'QQ Plot of Normal Datapoints')
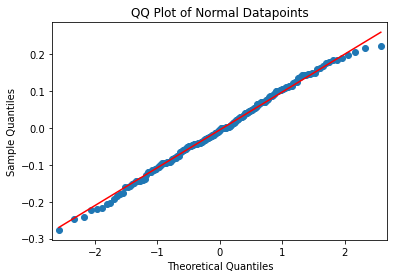
이상값 범위 나타내기
- 정규성 검정을 통해서 각 데이터가 이상값이 있다는 것을 파악했다면, 이번에는 이상값 범위를 정의한다.
- 연속형 변수의 이상값 범위는 1사분위-3사분위의 거리를 재는 것이다. 그 거리가 사분위범위의 1.5배를 넘으면 그 값을 이상값으로 간주한다.
thirdq = covid_case_df["total_cases"].quantile(0.75)
firstq = covid_case_df["total_cases"].quantile(0.25)
interquantile_range = 1.5 * (thirdq - firstq)
outlier_high = interquantile_range + thirdq
outlier_low = firstq - interquantile_range
print(outlier_low, outlier_high, sep = " <---> ")
-14736.125 <---> 25028.875
- 이상치를 제거한 데이터를 가져온다.
remove_out_lier_df = covid_case_df.loc[~(covid_case_df["total_cases"] > outlier_high) | (covid_case_df["total_cases"] < outlier_low)]
print(remove_out_lier_df.info())
<class 'pandas.core.frame.DataFrame'>
Index: 177 entries, AFG to ZWE
Data columns (total 5 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 location 177 non-null object
1 total_cases 177 non-null int64
2 total_deaths 177 non-null int64
3 total_cases_pm 177 non-null float64
4 total_deaths_pm 177 non-null float64
dtypes: float64(2), int64(2), object(1)
memory usage: 8.3+ KB
None
- 이제 두 데이터의 히스토그램을 비교해본다.
fig, ax = plt.subplots(figsize = (16, 6), ncols = 2)
ax[0].hist(covid_case_df["total_cases"]/1000, bins = 7)
ax[0].set_title("Total Covid Cases (thousands) for all")
ax[0].set_xlabel("Cases")
ax[0].set_ylabel("Number of Countries")
ax[1].hist(remove_out_lier_df["total_cases"]/1000, bins = 7)
ax[1].set_title("Total Covid Cases (thousands) for removed outlier")
ax[1].set_xlabel("Cases")
ax[1].set_ylabel("Number of Countries")
plt.show()

References
Walker, M. (2020). Python Data Cleaning Cookbook: Modern techniques and Python tools to detect and remove dirty data and extract key insights. Packt Publishing.
