Machine Learning Tutorial 02 - Regression (2)
I. 지도 학습 VS 비지도 학습
머신러닝은 크게 두 가지 유형으로 분류한다. 우선 아래 표를 보자.
| 구분 | 지도학습(Supervised Learning) | 비지도 학습(Unsupervised Learning) |
|---|---|---|
| 알고리즘(분석모형) | 회귀분석분류모형 | 군집분석 |
| 특징 | 정답을 알고 있는 상태에서 학습모형 평가 방법이 다양한 편 | 정답이 없는 상태에서 서로 비슷한 데이터를 찾아서 그룹화모형 평가 방법이 제한적 |
지도학습(Supervised Learning)은 종속변수(Dependent Variable) 선정이 매우 중요하며. 종속변수 선정과 함께 데이터 분석도 같이 병행이 된다. 그러나 비지도학습(Unsupervised Learning)은 데이터가 많은데, 어떻게 분류하면 좋을지 모를 때 서로 비슷한 특징끼리 결합 및 그룹화 하는 것을 말한다.
II. 회귀모형 예제
우선 회귀모형 모형부터 만들자. 아래 코드를 그대로 실행하면 될 것이다. 만약 파이썬(Python) 설치가 필요한 사람은 Tensorflow 2.0 Installation에서 설치 방법을 따라 설치를 진행하기를 바란다.
## 기본 라이브러리 불러오기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
<ipython-input-1-5e3e002ab9bf> in <module>
2 import pandas as pd
3 import numpy as np
----> 4 import matplotlib.pyplot as plt
5 import seaborn as sns
6 from sklearn.model_selection import train_test_split
ModuleNotFoundError: No module named 'matplotlib'
(1) No Module Names ’name_of_library'
가끔 이런 모듈이 없다고 나올 때가 있다. 이해하기 어려운 것은 아니다. 가장 좋은 것은 언제나 에러 메시지 전체를 복사해서 구글에서 검색을 한 뒤 해결책을 빠르게 찾는 것이 좋다.
위 에러는 matplotlib 모듈이 없다는 뜻이다.
그럼 설치를 해보자. 어떻게? 자세한 내용은 공식문서를 참고한다. matplotlib 간단한 설치방법은 아래와 같다.
터미널에서 아래와 같이 입력한다. 참고로 MacOS / 필자는 pip3로 설치할 예정이다. 윈도우 아나콘다 설치 버전
$ python3 -m pip install -U pip
$ python3 -m pip install -U matplotlib
matplotlib와 마찬가지로 seaborn 그리고 scikit-learn 모듈도 같이 위와 같은 형태로 설치를 하면 된다.
(2) Sample Tutorial
전체 소스코드를 실행한 뒤, 하나씩 간단하게 설명을 진행하도록 한다.
A. 데이터 수집
데이터 수집은 필자의 github에서 직접 가져온 것이다. 다운 받을 필요없이 아래 코드를 그대로 복사하면 사용하면 된다.
import io
import requests
import pprint
url = "https://raw.githubusercontent.com/chloevan/datasets/master/weather/Weather.csv"
url = requests.get(url).content
weather_df = pd.read_csv(io.StringIO(url.decode('utf-8')))
pprint.pprint(weather_df.head())
STA Date Precip WindGustSpd MaxTemp MinTemp MeanTemp \
0 10001 1942-7-1 1.016 NaN 25.555556 22.222222 23.888889
1 10001 1942-7-2 0 NaN 28.888889 21.666667 25.555556
2 10001 1942-7-3 2.54 NaN 26.111111 22.222222 24.444444
3 10001 1942-7-4 2.54 NaN 26.666667 22.222222 24.444444
4 10001 1942-7-5 0 NaN 26.666667 21.666667 24.444444
Snowfall PoorWeather YR ... FB FTI ITH PGT TSHDSBRSGF SD3 RHX RHN \
0 0 NaN 42 ... NaN NaN NaN NaN NaN NaN NaN NaN
1 0 NaN 42 ... NaN NaN NaN NaN NaN NaN NaN NaN
2 0 NaN 42 ... NaN NaN NaN NaN NaN NaN NaN NaN
3 0 NaN 42 ... NaN NaN NaN NaN NaN NaN NaN NaN
4 0 NaN 42 ... NaN NaN NaN NaN NaN NaN NaN NaN
RVG WTE
0 NaN NaN
1 NaN NaN
2 NaN NaN
3 NaN NaN
4 NaN NaN
[5 rows x 31 columns]
/Users/jihoonjung/Library/Python/3.7/lib/python/site-packages/IPython/core/interactiveshell.py:3063: DtypeWarning: Columns (7,8,18,25) have mixed types.Specify dtype option on import or set low_memory=False.
interactivity=interactivity, compiler=compiler, result=result)
pprint.pprint(weather_df.describe())
STA WindGustSpd MaxTemp MinTemp \
count 119040.000000 532.000000 119040.000000 119040.000000
mean 29659.435795 37.774534 27.045111 17.789511
std 20953.209402 10.297808 8.717817 8.334572
min 10001.000000 18.520000 -33.333333 -38.333333
25% 11801.000000 29.632000 25.555556 15.000000
50% 22508.000000 37.040000 29.444444 21.111111
75% 33501.000000 43.059000 31.666667 23.333333
max 82506.000000 75.932000 50.000000 34.444444
MeanTemp YR MO DA DR \
count 119040.000000 119040.000000 119040.000000 119040.000000 533.000000
mean 22.411631 43.805284 6.726016 15.797530 26.998124
std 8.297982 1.136718 3.425561 8.794541 15.221732
min -35.555556 40.000000 1.000000 1.000000 2.000000
25% 20.555556 43.000000 4.000000 8.000000 11.000000
50% 25.555556 44.000000 7.000000 16.000000 32.000000
75% 27.222222 45.000000 10.000000 23.000000 34.000000
max 40.000000 45.000000 12.000000 31.000000 78.000000
SPD ... FT FB FTI ITH PGT SD3 RHX RHN RVG \
count 532.000000 ... 0.0 0.0 0.0 0.0 525.000000 0.0 0.0 0.0 0.0
mean 20.396617 ... NaN NaN NaN NaN 12.085333 NaN NaN NaN NaN
std 5.560371 ... NaN NaN NaN NaN 5.731328 NaN NaN NaN NaN
min 10.000000 ... NaN NaN NaN NaN 0.000000 NaN NaN NaN NaN
25% 16.000000 ... NaN NaN NaN NaN 8.500000 NaN NaN NaN NaN
50% 20.000000 ... NaN NaN NaN NaN 11.600000 NaN NaN NaN NaN
75% 23.250000 ... NaN NaN NaN NaN 15.000000 NaN NaN NaN NaN
max 41.000000 ... NaN NaN NaN NaN 23.900000 NaN NaN NaN NaN
WTE
count 0.0
mean NaN
std NaN
min NaN
25% NaN
50% NaN
75% NaN
max NaN
[8 rows x 24 columns]
describe() - 주요 통계 정보를 확인할 수 있다.
B. 독립 및 종속변수 선정
X = weather_df['MinTemp'].values.reshape(-1,1) # 독립변수
y = weather_df['MaxTemp'].values.reshape(-1,1) # 종속변수
array([[22.22222222],
[21.66666667],
[22.22222222],
...,
[18.33333333],
[18.33333333],
[17.22222222]])
MinTemp의 값에 따라서 MaxTemp의 값이 어떻게 변하는지 예측하고자 한다. 따라서, MinTeamp는 독립변수, MaxTemp는 종속변수로 정했다.
이 때, .values.reshape(-1, 1)의 함수가 보일 것이다. 이 함수는 NumPy계열의 함수로서, Return값은 Array형태로 바꿔주는 역할을 한다. (참고: 파이썬은 기본적으로 행렬 연산에 근간을 둔다!)
여기에서는 .values.reshape(-1,1)에 대한 자세한 설명은 생략한다. 쉽게 말하면 데이터의 차원(Dimension)과 관련이 있다. 만약 궁금하다면, What does -1 mean in numpy reshape?글을 참고하기를 바란다.
C. 데이터 셋 분리
# 데이터 셋 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
print('train data: ', len(X_train), '개')
print('test data: ', len(X_test), '개')
train data: 95232 개
test data: 23808 개
데이터 셋을 분리하는 작업이다. 명시적으로 기억해두면 좋다. test_size는 검증 데이터의 비율을 의미하고, random_state는 랜덤 추출값과 관련이 있다.
D. 모형 학습
# 모형 개발 선언
regressor = LinearRegression()
regressor.fit(X_train, y_train) # 알고리즘 트레이닝
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
regressor = LinearRegression()는 모형객체(LinearRegression())를 생성해서 변수 regressor를 할당한다.
할당된 변수 regressor에 fit() 적용하는 코드다.
우리가 작업한 코드는 아래 수식을 따른다고 보면 된다.
\begin{align} \ Y= aX + b \end{align}
위 식에 대한 간단한 설명은 아래와 같다.
Y: 종속변수 (여기에서는 MaxTemp 값을 찾는 식)b: 상수=y절편a: 회귀계수=기울기X: 독립변수 (여기에서는 주어진 MinTemp 값을 대입하면 된다.)
Y값을 구하려면, 상수와 회귀계수(=기울기)만 구하면 된다. 독립변수의 값은 우리는 이미 알고 있다.
# intercept: 상수
print('상수 값: ', regressor.intercept_)
# slope: 회귀계수=기울기
print('회귀계수 값: ', regressor.coef_)
상수 값: [10.66185201]
회귀계수 값: [[0.92033997]]
E. 예측
모형을 만들었으니, 이제 본격적으로 예측을 진행하도록 한다.
# 예측
y_pred = regressor.predict(X_test)
# 데이터 셋 비교
pred_df = pd.DataFrame({'실제값': y_test.flatten(), '예측값': y_pred.flatten()})
pprint.pprint(pred_df.head())
실제값 예측값
0 28.888889 33.670351
1 31.111111 30.091251
2 27.222222 26.512151
3 28.888889 31.113851
4 23.333333 15.774852
# 테스트 데이터와 예측값의 기울기 비교
plt.scatter(X_test, y_test, color='gray')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.show()
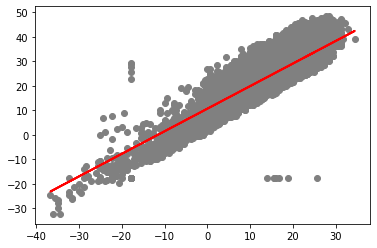
위 그래프를 보면 회귀선 라인의 방향성이 대체적으로 맞는 것을 볼 수가 있다. 회귀선은 위치한 각 점들의 정중앙을 통과하는 직선을 찾는 최소자승법을 이용한다.
F. 모형 성능 평가
회귀모형을 만든 이후에는 모형성능을 평가해야 한다. 회귀모형의 성능평가는 크게 3가지로 나타나는데, 크게 MAE, MSE, RMSE로 구분되어진다. 각각의 구체적인 차이점에 대해서는 추후에 작성해서 올리도록 하겠다. 각각의 차이점이 있기는 하지만, 가장 중요한 개념은 어떤 특정 모형의 예측값과 실제값의 차이가 얼마나 나는지 판단하는 것이고, 대중적으로 RMSE를 많이 사용한다.
다시 설명하면, 지금 만든 모형은 MinTemp를 변수를 가지고 MaxTemp를 예측하는 것이지만, 이 데이터는 30개의 독립변수 데이터를 가지고 있다. 즉, 단순회귀로만 접근한다면 30개의 모형을 만들어서 RMSE를 비교해서 각각의 차이를 봐야 하고, 또한 각 모형끼리 실제 통계적으로 유의한지도 따져 봐야 한다.
이러한 부분에 대한 방법은 매우 통계적 으로 접근해야 하기 때문에 추후 관련 포스팅을 하도록 하겠다. (아마 R로 기술하게 될 것 같다.)
파이썬에서는 아래와 같은 형태로 성능 평가를 간단하게 산출 할 수 있다.
# 모형 성능 평가
print('MAE:', metrics.mean_absolute_error(y_test, y_pred))
print('MSE:', metrics.mean_squared_error(y_test, y_pred))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
MAE: 3.19932917837853
MSE: 17.631568097568447
RMSE: 4.198996082109204
III. Reference
Chauhan, N. S. (2019, September 7). A beginner’s guide to Linear Regression in Python with Scikit-Learn. Retrieved March 19, 2020, from https://towardsdatascience.com/a-beginners-guide-to-linear-regression-in-python-with-scikit-learn-83a8f7ae2b4f
End of Document
