Deep Learning Loss Function
Page content
딥러닝 손실 함수 (Loss Function) 개요
딥러닝에서 손실 함수는 모델의 예측과 실제 값 사이의 차이를 측정하는 중요한 요소. 다양한 종류의 손실 함수가 있으며, 문제의 특성에 따라 적절한 함수를 선택해야 함.
주요 손실 함수 설명
평균 제곱 오차 (Mean Squared Error, MSE)
-
유형 : 회귀
-
공식 :
$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$
-
설명:
- $y_i$ : 실제 값
- $\hat{y}_i$ : 예측 값
- $n$ : 데이터 포인트의 수
-
사용 용도
- MSE는 회귀 문제에서 일반적으로 사용되며, 실제 값과 예측 값 간의 평균 제곱 차이를 최소화하는 것이 목표
- MSE는 큰 오류를 더 크게 벌점하기 때문에, 특히 이상치에 민감하게 반응.
- 이는 모델이 오류가 큰 예측에 대해 더 많이 조정되도록 만듬
평균 절대 오차 (Mean Absolute Error, MAE)
- 유형 : 회귀
- 공식 :
$$ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| $$
- 설명:
- $y_i$ : 실제 값
- $\hat{y}_i$ : 예측 값
- $n$ : 데이터 포인트의 수
- 사용 용도
- MAE는 MSE와 유사하게 회귀 문제에서 사용되지만, 오차를 제곱하지 않기 때문에 이상치에 덜 민감함.
- MAE는 오차의 크기를 선형적으로 반영하므로, 직관적으로 해석하기 쉬운 점이 장점입니다.
이진 교차 엔트로피 (Binary Cross-Entropy)
- 유형 : 이진 분류
- 공식 :
$$ \text{Binary Cross-Entropy} = -\frac{1}{n} \sum_{i=1}^{n} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] $$
- 설명:
- $y_i$ : 실제 라벨 (0 또는 1)
- $\hat{y}_i$ : 양성 클래스의 예측 확률
- $n$ : 데이터 포인트의 수
- 사용 용도
- 이진 교차 엔트로피는 이진 분류 문제에서 사용됨.
- 주어진 입력이 양성 클래스에 속할 확률을 예측하는 문제에서 주로 사용됨.
- 잘못된 예측에 대해 큰 패널티를 주는 특징이 있음.
범주형 교차 엔트로피 (Categorical Cross-Entropy)
- 유형 : 다중 클래스 분류
- 공식 :
$$ \text{Categorical Cross-Entropy} = -\sum_{i=1}^{n} \sum_{c=1}^{C} y_{i,c} \log(\hat{y}_{i,c}) $$
- 설명 :
- $y_{i,c}$ : 관측치 $i$에 대해 클래스 라벨 $c$가 올바른 분류인 경우의 지표 (0 또는 1)
- $\hat{y}_{i,c}$ : 관측치 $i$가 클래스 $c$에 속할 예측 확률
- $n$ : 데이터 포인트의 수
- $C$ : 클래스의 수
- 사용 용도
- 범주형 교차 엔트로피는 다중 클래스 분류 문제에서 사용됨.
- 출력이 다양한 클래스에 걸친 확률 분포인 경우에 사용됨.
- 목표는 예측된 분포와 실제 분포 간의 차이를 최소화하는 것임.
희소 범주형 교차 엔트로피 (Sparse Categorical Cross-Entropy)
- 유형 : 다중 클래스 분류
- 사용 용도 :
- 범주형 교차 엔트로피와 동일하게 멀티 클래스 분류에 사용
- 라벨이 원-핫 인코딩된 벡터 대신 정수로 제공될 때 사용.
- 이 손실 함수는 원-핫 벡터로 라벨을 변환하는 것이 계산적으로 비용이 많이 드는 대규모 데이터 세트를 처리할 때 특히 유용함.
- 모델은 정수 라벨로 직접 작업하므로 메모리 사용량을 줄일 수 있음.
Focal Loss
- 유형 : 분류 (클래스 불균형이 있는 시나리오에서 사용)
- 공식 :
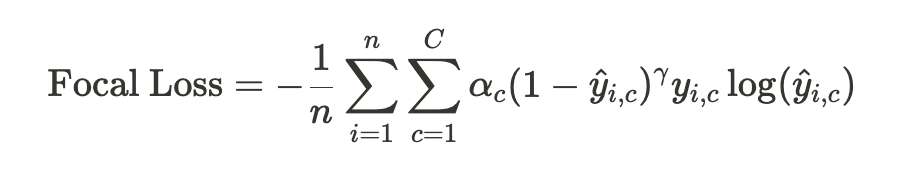
-
설명 :
- $y_{i,c}$ : 관측치 $i$에 대해 클래스 라벨 $c$가 올바른 분류인 경우의 지표 (0 또는 1)
- $\hat{y}_{i,c}$ : 관측치 $i$가 클래스 $c$에 속할 예측 확률
- $\alpha_c$ : 클래스 $c$에 대한 가중치 인자 (선택 사항, 클래스 불균형 해결을 위한 것)
- $\gamma$ : 쉬운 예제에 가중치를 낮추는 비율을 조정하는 포커싱 매개변수
- $n$ : 데이터 포인트의 수
- $C$ : 클래스의 수
-
사용 용도 :
- Focal Loss는 일부 클래스가 현저히 부족한 불균형 데이터 세트를 처리할 때 특히 유용함
- 불균한 데이터 세트에서는 전통적인 교차 엔트로피는 대다수 클래스에 편향될 수 있어 성능이 떨어질 수 있음.
- Focal Loss는 교차 엔트로피 기준에 $(1 - \hat{y}_{i,c})^\gamma$ 라는 조정 인자를 도입함.
- 이 조정 인자는 모델이 이미 자신 있는 쉬운 예제로부터 손실 기여도를 줄여 분류하기 어려운, 또는 잘못 분류된 예제에 더 집중하도록 조정
- $\gamma$ 매개변수는 쉬운 예제에 대해 얼마나 많이 가중치를 낮출지 결정함. $\gamma$ 값이 높을수록 어려운 예제에 더 집중하도록 함.
- 선택 사항인 $\alpha_c$ 항목은 특정 클래스에 더 많은 중요성을 부여하여 클래스 불균형 문제를 해결하는 데 도움을 줄 수 있음.
